ITEC 122 2007fall ibarland

home—info—lectures—hws—exams

hw12
FSMs; matching

Due Nov.30 (Fri) 17:00

1. Consider the grammar with production rules

   S → ε
   S → aSb
       

   Show how S can derive the string "aaabbb" (also known as a³ b³).
   Your answer will be of the form S ⇒                  ⇒                  ⇒ … ⇒ "aaabbb".
   (Recall that “ε” represents the empty string; Rosen uses “λ” for this same purpose.)
2. Some extra credit: prove that the preceding grammar can generate all strings of the form aⁿ bⁿ, for all n∈N.
   Why does this proof not show that the grammar generates exactly the language L' = { aⁿ  bⁿ | n∈N} ?
3. Draw the finite-state machine described by the following table:
   

   state	0	1
   s0	s1	s0
   s1	s0	s2
   s2	s1	s1

4. For the finite state machine drawn to the right, ignoring the second number on each arrow¹
   1. What state is the machine in, after the input sequence    "00110101"?
   2. What state is the machine in, after the input sequence "0100110101"?
   3. Describe the set of all strings which leave the machine in state s₂.
   Remember that for each input sequence, we start from the machine's start-state, s₀.



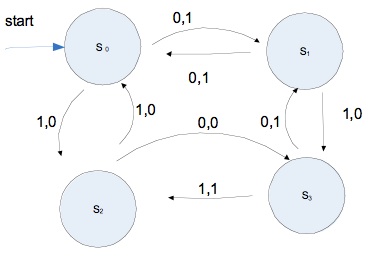
5. We'll model the progression of a volleyball game with a finite state machine. Our first attempt will be overly simplistic, but we'll add some features to arrive at a slightly less simplistic version.

   1. Let the set of states be
      S = { team1-to-serve, team1-to-return, team2-to-serve, team2-to-return }.
      (You can abbreviate these Srv1,Ret1,Srv2,Ret2.) Let the inputs be the set I = {Succeed,Fail} (you can abbreivate S,F), indicating a ref's call that the current state's action just succeeded or failed, resp. Thus we think of our model proceeding along the lines of:

      state:  team2-to-serve
      input:    Succeed         [indicates team 2 served successfully.]
      state:  team1-to-return2
      input:    Fail            [oops, team 1 failed to return the ball.]
      state:  team-2-to-serve
      ...
      

      Specify the 4-state FSM best modeling a volleyball game, where whenever a team fails, the other team gets to serve. Express your answer in table format.
   2. Give a new FSM which allows for the possibility of a "re-serve": If a team is to serve but fails, they get one further attempt³ before losing possession. You will need to add a little more state.
      Express your answer as a picture of a directed graph with labeled edges (as in lecture, similar to Rosen 11.2). Neatness improves clarity!
   3. Scoring in volleyball is interesting: only the team which served may score a point⁴ Our FSM won't actually keep track of score, but it will indicate when one team or the other scores a point, via two new states "increment-team1-score" and "increment-team2-score". (After an increment, the referee will always give the input S.)
      This requires quite a few more states.
6. Consider the Marriage Problem. Here is one example input: Four men (Alistair, Bernie, Corky, Dweezil -- abbreviated A,B,C,D resp.), and for women (Winnie, Xena, Yolanda, Zelda -- abbreviated W,X,Y,Z resp.). They each have the following preferences for marriage:

   Alistair:  W,X,Y,Z
   Bernie:    W,X,Z,Y
   Corky:     W,Y,Z,X
   Dweezil:   X,W,Y,Z
   
   Winnie:    A,B,C,D
   Xena:      C,B,D,A
   Yolanda:   D,B,A,C
   Zelda:     C,B,A,D
   

   The task is to come up with a pairing of each person with someone of the opposite gender.

   For example, one dating company, “HappyGuys” might come up with: A+W, B+X, C+Y, D+Z.

   Another company, “HappyGals” tried: A+W, C+X, D+Y, B+Z.

   1. Give an input with two men and two women, along with all possible solutions to your input.
   2. Give a second (fundamentally different) input with two men and two women.

   3. In the HappyGals solution to the example given above, what happens, when Bernie+Zelda happen to go out to the same restaurant as Corky+Xena?

   4. To think about for lecture:
      • Are some solutions better than others?
      • What are good properties for a solution to have?
      • How many solutions are possible, for an input with 2n people?
      • Is a brute-force solution feasible?

   Finally, consider The Suitor's Algorithm (phrased in medieval terms):

   • male strategy: go to the tower with his most-preferred woman who hasn't already spurned him, and stay as long as he's being flirted with.
   • female strategy: sit in her tower, and of all the suitors outside her window (if any), flirt with the highest preference, and spurn the rest.
   This repeats until there are no changes.
   We will talk about this algorithm in lecture, starting with the question of whether or not it is guaranteed to terminate.

home—info—lectures—hws—exams

©2007, Ian Barland, Radford University Last modified 2007.Dec.04 (Tue)

Please mail any suggestions (incl. typos, broken links) to iba�rlandrad�ford.edu