ITEC 122 2008fall ibarland

home—info—lectures—exams—archive

hw12
FSMs; matching

Due 2008.Dec.12 (Fri)

1. p.398, #4 (5ed p.360, #4)
   Remember: divide the number of "desired" outcomes by the number of possible outcomes.
   (We presume that each day is equally likely, out of the 366 possibilities).
2. p.398, #6 (5ed p.360, #6) When counting desired outcomes, be sure not to accidentally count the ace of hearts twice!
3. p.398, #8 (5ed p.361, #8)
4. (Extra credit; read §12.1, example 12)
   Consider the grammar with production rules

   S → ε
   S → aSb
       

   Show how S can derive the string "aaabbb" (also known as a³ b³).
   Your answer will be of the form "S" ⇒                  ⇒                  ⇒ … ⇒ "aaabbb".
   (Recall that “ε” represents the empty string; Rosen uses “λ” for this same purpose.)
5. Extra credit: prove that the preceding grammar can generate all strings of the form aⁿ bⁿ, for all n∈N.
   (How is this different from asking for a proof that the grammar generates exactly the language L' = { aⁿ  bⁿ | n∈N} ?)
6. Draw the finite-state machine described by the following table:
   

   state	0	1
   s0	s1	s0
   s1	s0	s2
   s2	s1	s1

7. For the finite state machine drawn to the right, ignoring the second number on each arrow¹
   1. What state is the machine in, after the input sequence    "00110101"?
   2. What state is the machine in, after the input sequence "0100110101"?
   3. Ignore this problem -- it is more difficult that intended, for this particular machine. Describe the set of all strings which leave the machine in state s₂.
   Remember that for each input sequence, we start from the machine's start-state, s₀.



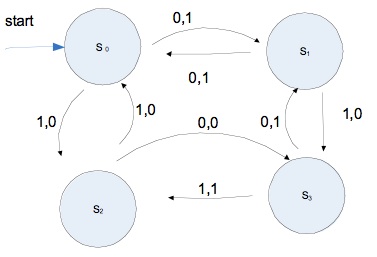
8. We'll model the progression of a volleyball game with a finite state machine. Our first attempt will be overly simplistic, but we'll add some features to arrive at a slightly less simplistic version.

   1. Let the set of states be
      S = { team1-to-serve, team1-to-return, team2-to-serve, team2-to-return }.
      (You can abbreviate these Srv1,Ret1,Srv2,Ret2.) Let the inputs be the set I = {Succeed,Fail} (you can abbreivate S,F), indicating a ref's call that the current state's action just succeeded or failed, resp. Thus we think of our model proceeding along the lines of:

      state:  team2-to-serve
      input:    Succeed         [indicates team 2 served successfully.]
      state:  team1-to-return2
      input:    Fail            [oops, team 1 failed to return the ball.]
      state:  team-2-to-serve
      ...
      

      Specify the 4-state FSM best modeling a volleyball game, where whenever a team fails, the other team gets to serve. Express your answer in table format.
   2. Give a new FSM which allows for the possibility of a "re-serve": If a team is to serve but fails, they get one further attempt³ before losing possession. You will need to add a little more state.
      Express your answer as a picture of a directed graph with labeled edges (as in lecture, similar to Rosen 11.2). Neatness improves clarity!
   3. Scoring in volleyball is interesting: only the team which served may score a point⁴ Modify our FSM from part (b) to handle this. (Our FSM won't actually keep track of score, but it will indicate when one team or the other scores a point, via two new states "increment-team1-score" and "increment-team2-score". After an increment, the referee will always give the input S.)
      This requires quite a few more states.
9. Consider the Marriage Problem: we'll introduce it with an example input: Four men (Alistair, Bernie, Corky, Dweezil -- abbreviated A,B,C,D resp.), and four women (Winnie, Xena, Yolanda, Zelda -- abbreviated W,X,Y,Z resp.), along with their preferences for hooking up marriage:

   Alistair:  W,X,Y,Z
   Bernie:    W,X,Z,Y
   Corky:     W,Y,Z,X
   Dweezil:   X,W,Y,Z
   
   Winnie:    A,B,C,D
   Xena:      C,B,D,A
   Yolanda:   D,B,A,C
   Zelda:     C,B,A,D
   

   The task is to come up with a pairing of each person with someone of the opposite gender.

   For example, one dating company, “HappyGuys” came up with the following solution: A+W, B+X, C+Y, D+Z.

   Another company, “HappyGals” arrived at a different solution: A+W, C+X, D+Y, B+Z.

   1. Give an input with two men and two women and their preferences. Then, provide all possible solutions to your input.
   2. Give a second (fundamentally different⁵) input with two men and two women. Remember, an input consists of the people and their preferences.
   3. Challenge Question: When there are 2 men and 2 women, how many different (non-isomorphic) inputs are there?

   4. In the HappyGals solution to the example given above, what happens, when Bernie+Zelda happen to go out dancing at the same club as Corky+Xena?

   5. To think about for lecture (no writing required):
      • Are some solutions better than others?
      • What are good properties for a solution to have?
      • How many solutions are possible, for an input with 2n people?
      • Is a brute-force solution feasible?

   Finally, consider The Suitor's Algorithm (phrased in medieval, rather sexist terms):

   • female strategy: sit in her tower, and of all the suitors outside her window (if any), flirt with the highest preference, and spurn the rest.
   • male strategy: go to the tower with his most-preferred woman who hasn't already spurned him, and stay as long as he's being flirted with.
   This repeats until there are no changes.
   We will talk about this algorithm in lecture, starting with the question of whether the Suitor's Algorithm is even guaranteed to terminate.

home—info—lectures—exams—archive

©2008, Ian Barland, Radford University Last modified 2008.Dec.11 (Thu)

Please mail any suggestions (incl. typos, broken links) to iba�rlandrad�ford.edu