Recursive Algorithms and Recurrence Equations

Introduction

Initial Conditions

Up and Down Substitution

Closed Form

Overview

• Performance of recursive algorithms typically specified with recurrence equations


• Recurrence Equations aka Recurrence and Recurrence Relations
• Recurrence relations have specifically to do with sequences (eg Fibonacci Numbers)


• Recurrence equations require special techniques for solving


• We will focus on induction and the Master Method (and its variants)
• And touch on other methods

Analyzing Performance of Non-Recursive Routines is (relatively) Easy

• Loop: T(n) = $\Theta(n)$

    for i in 1 .. n loop
    

• Loop: T(n) = $\Theta(n^2)$

    for i in 1 .. n loop
        for j in 1 .. n loop
        end loop;
    end loop;

    for i in 1 .. n loop
        for j in 1 .. i loop
        end loop;
    end loop;
    

• Loop: T(n) = $\Theta(n^3)$ ... obvious

Analyzing Recursive Routines

• Analysis of recursive routines is not as easy: consider factorial

    fac(n) is
        if n = 1 then return 1
        else return fac(n-1) * 1
    

• How many times is fac called for fac(n)?


• To find an answer, Use a recurrence

Recurrences

• A recurrence defines T(n) in terms of T for smaller values


• Example: T(n) = T(n-1) + 1
• T(n) is defined in terms of T(n-1)


• Recurrences are used in analyzing recursive algorithms


• AKA: Recurrence Equation, Recurrence Relation

Evaluating a Recurrence

• How to think about T(n) = T(n-1) + 1


• How to find the value of a T(k) for a particular k:
• Substitute up from T(1) to T(k)
• Substitute down from T(k) to T(1)


• Solving the recurrence and evaluate the resulting expression


• All three methods require having the initial conditions for the recurrence

Initial Conditions

• The initial conditions are the values of the recurrence for small values of n


• For example, the values of T(0), T(1), T(2)


• We will see that the initial conditions are determined by the specific problem being solved
• A Recurrence Equation has multiple solutions,
• The initial conditions determines which of those solutions applies.

Substituting Up and Down

• Problem: Find value of T(n) = T(n-1) + 1 for n=4, with initial condition T(1)=2


• Substituting up from T(1):
• T(1) = 2, Initial condition
• T(2) = T(1) + 1 = 2+1 = 3
• T(3) = T(2) + 1 = 3+1 = 4
• T(4) = T(3) + 1 = 4+1 = 5


• Subsituting down from T(4):
• Example: T(4) = T(3) + 1 = [T(2) + 1] + 1 = [[T(1) + 1] + 1] + 1 = 2+1+1+1 = 5

Solving the Recurrence: Closed Forms

• To solve a recurrence, we find a closed form for it
• Closed form for T(n): An equation that defines T(n) using an expression that does not involve T
• Example: A closed form for T(n) = T(n-1)+1 is T(n) = n.


• Solution techniques - no single method works for all:
• Guess and Check
• Forward substitution
• Backward Substitution
• Characteristic equation


• Master method (2 versions)
• Recurrence trees help us think about recurrences and show intuition in Master Method

Solving RE

Forward and Backward Substitution, Initial Conditions

Guess and Check: Forward Substitution

• Recurrence: T(n) = T(n-1) + 1, with initial condition t(1) = 2
• Look for a pattern:
• T(1) = 2, Initial condition
• T(2) = T(1) + 1 = 2+1 = 3
• T(3) = T(2) + 1 = 3+1 = 4
• T(4) = T(3) + 1 = 4+1 = 5
• T(5) = T(4) + 1 = 5+1 = 6
• Guess:
• T(n) = n + 1


• Informal Check:
• T(n) = T(n-1)+1 = [(n-1)+1] + 1 = n+1
• T(1) = 1+1 = 2


• Informally: a closed form is correct if it satisfies the open form and the initial conditions


• Formally: Prove the closed form is correct using induction (example below)

Guess and Check: Backward Substitution

• Look for a pattern (how many 1's in each line?):
• T(n) = T(n-1) + 1
• T(n) = [T(n-2)+1] + 1
• T(n) = [[T(n-3)+1]+1] + 1
• T(n) = [[[T(n-4)+1]+1]+1] + 1
• ...
• T(n) = [...[[T(n-k)+1]+1] ... +1] + 1 [has k ones]
• ... [Let k = n-1]
• T(n) = [...[[T(n-(n-1))+1]+1] ... +1] + 1 [has k=n-1 ones]
• T(n) = T(n-(n-1)) + (n - 1)
• T(n) = T(1) + (n-1)
• T(n) = 2 + (n - 1)
• T(n) = n + 1
• This process leads to this Guess:
• T(n) = n + 1


• Check the guess, by substituting, as in the previous example:
• T(n) = T(n-1)+1 = [(n-1)+1] + 1 = n+1
• T(1) = 1+1 = 2

Recurrences Without Initial Conditions

• A recurrence without initial conditions is satisfied by a family of closed forms


• Example: Recurrence T(n) = T(n-1) + 1 is satisfied by each member of this family of closed forms:
• T(n) = n
• T(n) = n + 1
• T(n) = n + 2
• ...
• T(n) = n - 1
• T(n) = n - 2
• ...


• With specific initial conditions, only one of that family satisfies both the recurrence and the initial conditions


• Example: Recurrence T(n) = T(n-1) + 1 with Initial Condition T(1) = 1 is satisfied by:
• T(n) = n
• Example: Recurrence T(n) = T(n-1) + 1 with Initial Condition T(1) = 0 is satisfied by:
• T(n) = n - 1

Initial Conditions and Solutions - More Examples

• The solution to a recurrence is determined by its initial condition
• Example 1:
• T(n) = T(n-1) + 1
• T(1) = 2
• Guess: T(n) = n + 1
• Check: as above
• T(n) = T(n-1)+1 = [n-1+1] + 1 = n+1
• T(1) = 1+1 = 2


• Example 2:
• T(n) = T(n-1) + 1
• T(1) = 1
• Guess: T(n) = n
• Check, as above:
• T(n) = T(n-1)+1 = [n-1] + 1 = n
• T(1) = 1


• Initial conditions restrict number of solutions
• In this case, restricts to one condition

Recurrence Equations for Sample Algorithms

Performance of Recursive Routines

• Let's develop recurrences for some recursive algorithms:
• Factorial
• Fibonacci
• Binary Search
• Towers of Hanoi


• What shall we count: number of calls, number of multiplies, ...

Performance of Factorial

• Algorithm:

    fac(n)
        if n = 1 return 1  
        else return n * fac(n-1)
    

• For fac(n), how many times is fac called?
• T(n) = T(n-1) + 1
• T(1) = 1


• $T(n) = n$


• Whatever the number of calls is for n-1 is, the calls for n is one larger

Performance of Factorial, revisited

• For fac(n), how many multiplies?
• T(n) = T(n-1) + 1
• T(1) = 0


• Guess: T(n) = ???
• Check: ...

Performance of Fibonacci

• Algorithm:

    fib(n)
        if n in 1 .. 2 return 1  
        else return fib(n-1) + fib(n-2)
    

• For fib(n), how many times is fib called?
• $T(1) = 1$
• $T(2) = 1$
• $T(3) = T(1) + T(2) + 1 = 1 + 1 + 1 = 3 $
• $T(4) = T(3) + T(2) + 1 = 3 + 1 + 1 = 5 $
• $T(5) = T(4) + T(3) + 1 = 5 + 3 + 1 = 9 $


• $T(n) = T(n-1) + T(n-2) + 1 $


• $T(n) = ?$ [This one's not so easy]
• The text shows that this has exponential behavior
• Book also uses T(0) = 0 as an initial condition.

Performance of Recursive Binary Search

• Algorithm (n?, count?):

    index binsearch(index low, high, keytype S[], keytype x)
        if low ≤ high then
            mid = (low + high) / 2
            if x = S[mid] then
                return mid
            elsif x < s[mid] then
                return binsearch(n, low, mid-1, S, x)
            else
                return binsearch(n, mid+1, high, S, x)
        else
            return 0
    end binsearch
    

• For binsearch(n), how many times is binsearch called in the worst case?


• T(0) = 1
• T(1) = 2
• T(2) = T(1) + 1 = 3
• T(4) = T(2) + 1 = 4
• T(8) = T(4) + 1 = 4 + 1 = 5


• T(n) = T(n/2) + 1


• Guess: $T(n) = \lg n + 2$ for $n=2^k$
• Informal Check:
$\begin{align*} T(n) & = T(n/2) + 1 \\ & = (\lg \frac{n}{2} + 2) + 1 \\ & = (\lg n - \lg 2 + 2) + 1 \\ & = (\lg n - 1 + 2) + 1 \\ & = \lg n + 2 \end{align*} $
• We can prove $T(n) = \lg n + 2$ by induction ...
• $T(n) = \Theta(\lg n)$
• What do we assume about n?

Towers of Hanoi

• Recursive algorithm
• Recurrence Equation: T(n) = ...
• Closed form: ...

More Example Algorithms and their Recurrence Equations

• More Eamples - Let's review or figure out these:
• Factorial (Every Case):


• Fibonacci (Every Case):


• Binary Search (Worst Case):


• Quick Sort (Worst Case):


• Quick Sort(Best Case):


• Merge Sort(Every Case):

More Example Algorithms and their Recurrence Equations

• More Eamples - Let's review or figure out these:
• Factorial (Every Case): $T(n) = T(n-1) + 1$


• Fibonacci (Every Case): $T(n) = T(n-1) + T(n-2) + 1$


• Binary Search (Worst Case): $T(n) = T(n/2) + 1$


• Quick Sort (Worst Case): $T(n) = T(n-1) + \Theta(n)$


• Quick Sort(Best Case): $T(n) = 2T(\frac{n}{2}) + \Theta(n)$


• Merge Sort(Every Case): $T(n) = 2T(\frac{n}{2}) + \Theta(n)$


• General Forms:
• $T(n) = aT(\frac{n}{b}) + f(n)$
• $T(n) = aT(n - b) + f(n)$

Technical Issues and Θ on RHS

Technical Issues

• Floors and Ceilings
• Usually Ignore
• Or assume size is power of 2


• Initial (or Boundary) conditions
• Frequently we use asymptotic values
• Example: $T(1) = \Theta(1)$


• Exact vs asymptotic functions
• Usually asymptotic is good enough
• Finding exact solutions requires exact boundary conditions

$\Theta(n)$ on the RHS

• In $T(n) = T(n-1) + \Theta(n)$, the $\Theta(n)$ terms refers to some function in $\Theta(n)$
• That is, $f(n) \in \Theta(n)$


• In most cases, the exact function does not affect the asymptotic behavior of $T(n)$


• This allows us to simplify by ignoring the exact function

Solution Techniques

Recurrence Equations - Solution Techniques

• No simple way to solve all recurrence equations


• Following techniques are used:
• Guess a solution and use induction to prove its correctness
• Use Forward and Backward Substitution to guess, if needed


• Use a general formula (ie the Master Method)
• For $T(n) = aT(\frac{n}{b}) + cn^k$ [Version in Text]


• For $T(n) = aT(\frac{n}{b}) + f(n)$ [More general version, NIB, but in CLR


• Solve using Characteristic Equation
• Linear homogeneous equations with constant coefficients
• Non-linear homogeneous equations with constant coefficients


• Change of Variable


• We focus on the general formulae and touch on the others
• General formulae can be understood using recursion trees
• First we see an example of induction

Checking Recurrence Closed Forms Using Induction

Check Using Induction: Factorial [SKIP]

• For fac(n), how many times is fac called (every case)?
• Above we derived:
• T(1) = 1
• T(k) = T(k - 1) + 1


• T(n) = n


• Inductive proof that $T(n) = n \text{ is a solution of }T(n) = T(n-1) + 1$, with initial condition T(1)=1:
1. Base Case: Prove $T(n) = n \text{ is a solution }$ for n = 1. T(1) = 1 is an initial condition.
2. Inductive Step: Prove: For all $n \gt 1, T(n) = n \text{ is a solution} \implies T(n+1) = n+1$ is a solution
• Inductive Hypothesis: $T(n) = n$ is a solution
• Now consider T(n) + 1:
$\begin{align*} T(n+1) & = T((n+1)-1) + 1 \\ & = T(n) + 1 \\ & = n + 1\textrm{, by IH} \\ \end{align*} $
• This proves the Inductive Step
3. Therefore from 1 and 2, by induction, we conclude that $T(n) = n \text{ for all } n ≥ 1$

Example Using Induction: Binary Search [SKIP]

• Worst case number of calls of binary search (assume n is a power of 2
• Recurrence: $T(n) = T(n/2) + 1 \text{ with } T(1)=2 $ [Derived above]


• Closed form: $T(n) = \lg n + 2$ [Guessed above.]


• Inductive proof that closed form is solution for recurrence (assume powers of 2):
1. Base Case: Prove for 1: $T(1) = \lg 1 + 2 = 0 + 2 = 2$.
2. Inductive Step: Prove: that $T(k) = \lg k + 2, \textrm{ for all } k < n$
3. Inductive Step: Prove: For all $n \gt 1, T(n) = \lg n + 2, \text{ is a solution} \implies T(2n) = \lg 2n +2 = \lg n +3$ is a solution
• IH: Assume that $T(k) = \lg k + 2, \textrm{ for all } k < n$
• Now consider $T(2n)$:
$\begin{align*} T(2n) & = T(2n/2) + 1\text{, by recurrence} \\ & = T(n) + 1 \\ & = (\lg n + 2) + 1, \text{ by IH} \\ & = \lg n + 3 \end{align*} $
• This proves the Inductive Step


4. Therefore from 1 and 2 we conclude that $T(n) =\lg n +2 \text{ is a solution to the recurrence for all } n ≥ 1$, where n is a power of 2
• Can also be proved for non-powers of 2

Master Method

Master Method from Text

• Cookbook way of solving recurrences of this form:
• $T(n) = aT(\frac{n}{b}) + \Theta(n^d)$
• $T(1) = c$


• $n = b^k$, for positive integer $k$
• $a \ge 1, b \ge 2, c \gt 0, d \ge 0$ are constants


• $ T(n) \in \begin{cases} \Theta(n^d), & a < b^d \\ \Theta(n^d\lg n), & a = b^d \\ \Theta(n^{\log_b a)}, & a > b^d \end{cases} $


• We call these Case 1, Case 2, and Case 3.


• Intuition: Which term of recurrence dominates (ie contributes more)


• In the recurrence we can replace "T(n)=" with "T(n)≤" or "T(n)≥" and get $O$ or $\Omega$ performance

Examples using Master Method from Text

• $T(n) = 16T(n/4) + 5n^3$
• $a=16, b=4, d=3$
• 16 < 4³ and so Case 1
• Thus, $T(n) = \Theta(n^d) = \Theta(n^3)$


• $T(n) = 2T(n/2) + n$
• $a=2, b=2, d=1$
• 2 = 2¹ and so Case 2
• Thus, $T(n) = \Theta(n^1\lg n)$


• $T(n) = 8T(n/2) + n$
• $a=8, b=2, d=1$,
• 8 > 2¹ and so Case 3
• Thus, $T(n) = \Theta(n^{\log_b a}) = \Theta(n^{\lg 8}) = \Theta(n^3)$

General Master Method [Not In Book]

• Solve $T(n) = aT(\frac{n}{b}) + f(n)$
• The MM in the text is a special case version of this one
• Text's MM's 3 cases are special cases of the GMM 3 cases


• $ T(n) \in \begin{cases} \Theta(f(n)), & f(n) = \Omega(n^{log_b a+\epsilon}) \text{ and } af(n/b) ≤ cf(n) \text{ for some constant } c ≤ 1 \text{ and large } n \\ \Theta(n^{\log_b a}\lg n), & f(n) = \Theta(n^{log_b a})\\ \Theta(n^{\log_b a)}, & f(n) = O(n^{log_b a-\epsilon}) \end{cases} $


• Assume $0 < \epsilon$


• Case 1 can also be written as $n^{log_b a+\epsilon} = O(f(n))$
• We ignore Case 1 because of its more complex condition

Examples

• $T(n) = 2T(n/2) + n$
• $a=2, b=2, f(n)=n, \log_b a = \lg 2 = 1$
• Case 2: $f(n) = n = n^1 = \Theta(n^{\log_b a})$
• Thus, $T(n) = \Theta(n^{\log_b a}\lg n) = \Theta(n \lg n)$


• $T(n) = 8T(n/2) + n$
• $a=8, b=2, f(n)=n, \log_b a = \log_2 8 = 3$
• Case 3: $f(n) = n = O(n^{3-1})$, with $\epsilon=1$
• Thus, $T(n) = \Theta(n^{\log_b a}) = \Theta(n^{\lg 8}) = \Theta(n^3)$

Text's Master Method vs General MM

• The text's Master Method is a special case of the general Master Method:


• Assume $T(n) = aT(n/k) + \Theta(n^d)$ meets the conditions for the Text's Case 2, ie $a = b^k$.
• Taking log of both sides of $a = b^d$ gives $log_b a = log_b b^d = d$.
• Thus, $f(n) \in \Theta( n^d)$ means $cn^{log_b a} \in \Theta(n^{log_b a})$ which is the condition for Case 2 in the General Master Method.
• Therefore, if a recurrence meets Case 2 of the Text's MM, then it also meets Case 2 of the General MM.
• Similar arguments can be made for the other cases.

Other Solution Techniques

Other Methods for Solving Recurrence Equations

• Characteristic Equation
• Linear homogeneous equations with constant coefficients
• Non-linear homogeneous equations with constant coefficients


• Change of Variable


• Substitution


• We look at briefly at the first and ignore the second two

Characteristic Equations

Homogenous Linear Recurrence Equations

• General form: $a_0t_n + a_1t_{n-1} + \dots + a_kt_{n-k} = 0$
• Slightly different from previous recurrence equations:
• Notation: $t_n$ vs $T(n)$
• all $t$ terms on LHS of equation
• 0 on RHS of equation


• Overview of how to solve:
• Assume $t_n = r^n$ is a solution for all $n$ and for some real number r


• Generate Characteristic Equation:
  • Recurrence: $a_0t_n + a_1t_{n-1} + \dots + a_kt_{n-k} = 0$
  • Substitute $r^n$ for $t_n$: $a_0r^n + a_1r^{n-1} + \dots + a_kr^{n-k} = 0$
  • Factor out $r^{n-k}$: $(r^{n-k})(a_0r^k + a_1r^{k-1} + \dots + a_kr^{k-k}) = 0$
  • Divide by $r^{n-k}$ (since it gives a root of r=0, which is not useful)
  • Resulting Characteristic Equation: $a_0r^k + a_1r^{k-1} + \dots + a_kr^{k-k} = 0$
  
  
• Find roots of Characteristic Equation


• Use roots of Characteristic Equation to form recurrence solution

Homogenous Linear Recurrence Equation: Example

• Notation: $t_n$ vs $T(n)$


• Recurrence:
• $t_n - 5t_{n-1} + 6t_{n-2} = 0$
• $t_0 = 0$
• $t_1 = 1$


• Assume $t_n = r^n$ is a solution, for all $n$ and for some real number r


• Substitute: $r^n - 5r^{n-1} + 6r^{n-2} = 0$


• Factor: $ r^{n-2}(r^2 - 5r^1 + 6r^0) = 0$


• Divide by $ r^{n-2}$ (since it gives a root of r=0, which is not useful)
• Resulting Characteristic Equation (CE): $r^2 - 5r^1 + 6r^0 = 0$


• Find roots of CE: $r^2 - 5r^1 + 6r^0 = (r-3)(r-2) = 0$
• Roots are 3 and 2
• That is, $r^2 - 5r^1 + 6r^0 = 0$ when $r_1=3$ or $r_2=2$


• By assumption, $t_n=3^n$ and $t_n=2^n$, are both solutions to the RE (and $t_n=0$, which we ignore).


• (Can verify that T(n) = 5T(-1) -6T(n-2) holds for each solution.)
• Since $t_n=3^n$ and $t_n=2^n$, are both solutions, so is the linear combination: $t_n = \alpha r_1^n + \beta r_2^n= \alpha 3^n + \beta 2^n$
• Plugging general solution into recurrence and distributing will give 0
• General solution defines an infinite number of solutions
• Use initial conditions to find a single solution
• If roots are identical, use this equation: $t_n = \alpha r^n + \beta nr^n$


• Choose $\alpha$ and $\beta$ to meet the initial conditions: $t_0=0,t_1=1$
• $t_0 = \alpha 3^0 + \beta 2^0 = 0$
• $t_1 = \alpha 3^1 + \beta 2^1 = 1$
• Solving gives: $\alpha=1$ and $\beta = -1$


• Thus: general solution is $t_n = \alpha 3^n + \beta 2^n== 3^n - 2^n$

Homogenous Linear Recurrence Equation: Fibonacci Numbers

• Recurrence:
• $T(n) = T(n-1) + T(n-2)
• $t_n - t_{n-1} - t_{n-2} = 0$
• $t_0 = 0$
• $t_1 = 1$


• Assume solution is of form $t_n = r^n$, for all $n$


• Substitute: $r^n - r^{n-1} - r^{n-2} = 0$


• Factor: $ r^{n-2}(r^2 - r^1 - r^0) = 0$


• Divide by $ r^{n-2}$ give CE: $r^2 - r^1 - r^0 = 0$


• Roots of CE: $(1+\sqrt{5})/2=\phi$ and $(1-\sqrt{5})/2=1-\phi = 1/\phi = \hat{\phi}$


• Choose $\alpha$ and $\beta$ to meet the initial conditions: $t_0=0,t_1=1$
• $t_0 = \alpha \phi^0 + \beta \hat{\phi}^0 = 0$
• $t_1 = \alpha \phi^1 + \beta \hat{\phi}^1 = 1$
• Solving gives: $\alpha=1/\sqrt{5}$ and $\beta = -1/\sqrt{5}$


• Thus: general solution is $t_n = \alpha \phi^n + \beta \hat{\phi}^n = \frac{1}{\sqrt{5}}(\phi^n - \hat{\phi}^n)$

Non-homogenous Linear Recurrence Equations

• General form: $a_0t_n + a_1t_{n-1} + \dots + a_kt_{n-k} = c \ne 0$


• RHS ≠ 0
• General plan:
• Find roots of related homogeneous equation and find alpha and beta.
• Form equation (eg $t_n = \alpha r_1^n + \beta r_2^n$ if distinct roots) and solve for alpha and beta
• Solution to non-homogeneous is based on solution to homogeneous
• We mostly ignore these

Change of Variable

• Substitute, for example, $2^k$ for $n$
• Example: For Fibonacci, number of additions
• $t_n = t_{n-1} + t_{n-2} + 1 = 0$
• $t_n - t_{n-1} - t_{n-2} = 1 $
• $t_n - t_{n-1} - t_{n-2} -1 = 0 $
• Substitute: $u_n = t_n + 1$
• We mostly ignore these

Recursion Tree - Intuition for Master Method

Recursion Tree

• A Recursion Tree is a technique for calculating the amount of work expressed by a recurrence equation
• Nice illustration of a recurrence
• Gives intuition behind Master Methods


• Each level of the tree shows the non-recursive work for a given parameter value
• See diagram


• Write each node with two parts:
• Upper part: $T(s)$ for some $s$
• Lower part: non-recursive part of $T(s)$


• Relation between parts: Upper part = lower part + upper parts of children

Example Recursion Tree

• Consider $T(n) = 2T(\frac{n}{3}) + 5n$
• $T(0) = 7$
• These values don't represent a specific algorithm. They are just chosen for illustration.


• First rewrite as $T(s) = 5s + 2T(\frac{s}{3})$
• Putting non-recursive term first is (slightly) easier
• Using a different variable allows us to focus on calculating $T(n)$


• Now calculate $T(27) = T(3^3)$:
• Root is $T(27)$:
• Upper part: $T(27)$
• Lower part: $5s=5\times 27 = 135$


• Children of root:
• How many children?
• What's in each child?


• Calculating $T(27)$:
$\begin{align*} T(27) & = 5\times 27 + 2 \times T(27/3) \\ & = 135 + 2 \times T(27/3) \\ & = 135 + 2 \times [45 + 2 \times T(9/3)] \\ & = 135 + 2 \times [45 + 2 \times [15 + 2 \times T(3/3)]] \\ & = 135 + 2 \times [45 + 2 \times [15 + 2 \times 7]] \\ & = 135 + 2 \times [45 + 2 \times 29] \\ & = 135 + 2 \times 103 \\ & = 135 + 206 \\ & = 341 \end{align*} $

Example Recursion Tree

• Consider $T(s) = 2T(\frac{s}{3}) + 5s = 5s + 2T(\frac{s}{3}) $
• Calculate $T(27)$

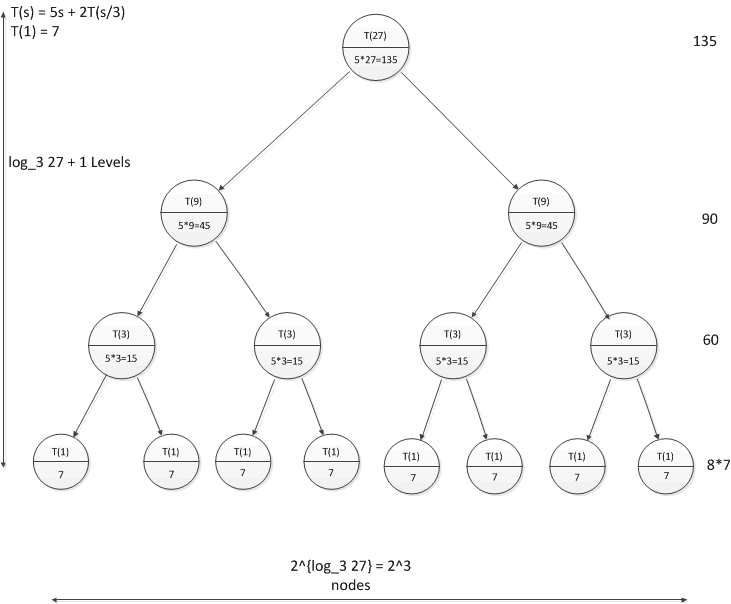
• Where do 2, 3, log₃, log₃ 27 come from?

Tree Properties

• Consider $T(s) = 5s + 2T(\frac{s}{3}) $


• Bottom level is level $\log_3 27$ = level 3
• Number of levels: $ 1 + \log_3 27 = 1 + 3 = 4$


• Sum of level 0: $2^0 \times (5\times 27) = 135$
• Sum of level 1: $2^1 \times (5\times 9) = 90$
• Sum of level 2: $2^2 \times (5\times 3) = 60$


• Sum of bottom level: $2^{\log_3 27} * 7 = 2^3 \times 7 = 56$


• Sum of all levels: $135 + 90 + 60 + 56 = 341$

Recursion Tree for $T(n) = aT(\frac{n}{b}) + f(n)$

• Recurrence Equation: $T(s) = f(s) + a T(s/b)$
• $T(1) = d$
• Find $T(n)$

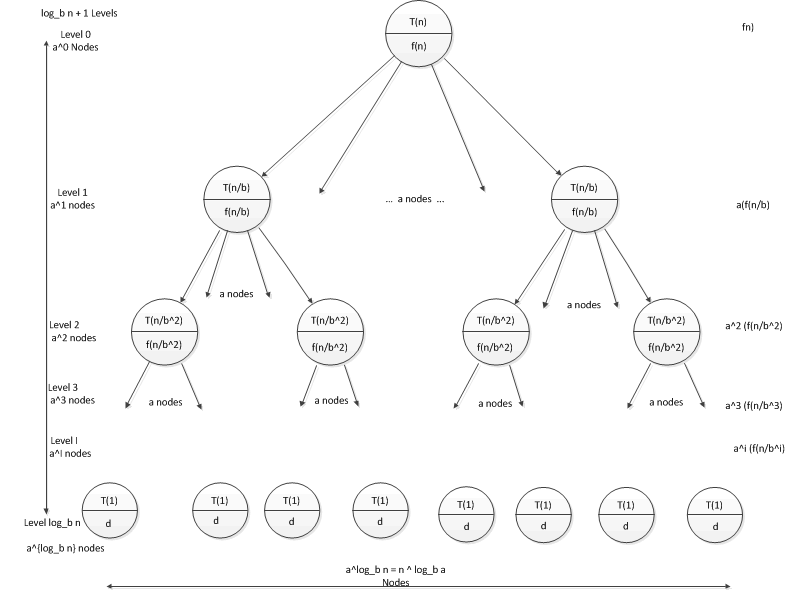
Summing the Values in the Tree

• Recurrence Equation: $T(s) = f(s) + a T(s/b)$
• $f(0) = d$


• Bottom level is level $\log_b n$
• Number of levels: $ 1 + \log_b n$


• Sum of all levels except leaves: cost of dividing and joining
• Sum of level 0: $a^0 \times f(\frac{n}{b^0}) $
• Sum of level 1: $a^1 \times f(\frac{n}{b^1}) $
• Sum of level 2: $a^2 \times f(\frac{n}{b^2}) $


• Sum of level i: $a^i \times f(\frac{n}{b^i}) $


• Sum of all levels except leaves: $\sum_{i=0}^{\log_b n - 1} a^i f(\frac{n}{b^i})$


• Sum of bottom level: cost of solving all problems of size 1
• $d a^{log_b n} = d n^{log_b a} $


• Sum of all levels:
$$ \sum_{i=0}^{\log_b n - 1} a^i f(\frac{n}{b^i}) + d n^{log_b a} $$

Fine Points

• $a ≥ 1, b > 1, \text{ are constants}$


• If $n$ is not a power of $b$, then replace $n/b$ by $\lfloor n/b \rfloor$ (or $\lceil n/b \rceil$)
• It can be proved that this does not affect the complexity

Evaluating the Complexity of the Sum of the Tree Levels

• Sum of all levels: $\displaystyle \sum_{i=0}^{\log_b n - 1} a^i f(\frac{n}{b^i}) + \Theta(n^{log_b a}) $


• Simplify base case of recursion using $\Theta(1)$ instead of $d$


• When this formula is a polynomial in $n$, we can simplify it by considering the power of $n$ in each term:
• Either first or second term can dominate or they can be the same order


• Intuitively:
• $\Theta(f(n))$, if the first term (ie the sum of non-leaf levels) dominates (Case 1)
• $\Theta(n^{log_b a}\lg n )$, if neither term dominates
• $\Theta(n^{log_b a})$, if the second term (ie sum of leaves) dominates (Case 3)
• Some restrictions occur


• These results can be formalized to obtain the General Master Method

Formalizing Gives the General Master Method

• To formalize, we consider the relation between the terms of the sum of the levels.


• Sum of all levels: $\displaystyle \sum_{i=0}^{\log_b n - 1} a^i f(\frac{n}{b^i}) + \Theta(n^{log_b a}) $


• Formal definition of one term dominating is below (assume $0 < \epsilon$):


• $\Theta(f(n))$, if $f(n) = \Omega(n^{log_b a+\epsilon})$ and $af(n/b) ≤ cf(n)$ for some constant $c ≤ 1$ and large $n$ [ie Case 1: second term (sum of non-leaves) dominates]


• $\Theta(n^{log_b a}\lg n )$, if $f(n) = \Theta(n^{log_b a})$ [ie neither term dominates]


• $\Theta(n^{log_b a})$, if $f(n) = O(n^{log_b a-\epsilon})$ [ie Case 3: second term (sum of leaves) dominates]
• This can also be written as $n^{log_b a+\epsilon} = O(f(n))$
• We ignore this case


• These results give the general Master Method