Maximal Subarray - Linear Algorithm
Overview
- This algorithm illustrates using a solution to a smaller problem in a solution to
a larger problem
First Example: Maximal Subarray
- Problem: Find maximal subarray in array X(1 .. $n$)
- Given integers $x_1, x_2, ..., x_n$,
find $a ≤ b$ that give $\displaystyle \text{max} \left(\sum_{i=a}^b x_i\right)$
- That is: find largest sum of a subsequence
- Solutions:
- Naive algorithms: $O(n^3)$ and $O(n^2)$ (ie triple and double loops)
- Divide and conquer algorithm: $O(n\lg n)$
- Dynamic Programming (DP) algorithm: $O(n)$
- Let's work though developing the DP algorithm
DP Maximal Subarray Algorithm: Assumptions
- Assume the following:
- Your algorithm examines each position 1 .. $n$
- You are currently examining position $p$
- In other words, you are working on subproblem $p$
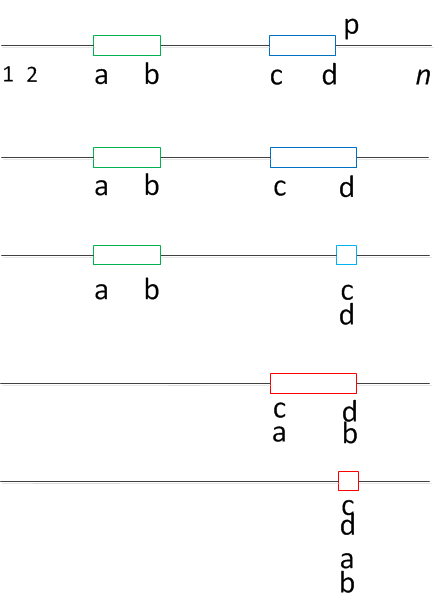
- The maximal subarray in 1 .. $p-1$ is at $a .. b$
- How could you use the maximal subarray in $1 .. p-1$ to find the maximal subarray
in $1..p$?
Using the Subproblem to Solve the Problem
- Consider finding the maximal subarray in elements $x_1 .. x_p$ for $ 2 ≤ p ≤ n$
- Subproblem solution: assume the maximal subarray in elements 1 .. $p-1$ is at $a .. b$
- There are two cases for $a .. b$?
- $a .. b$ reaches $p-1$ (ie $b=p-1$)
- $a .. b$ does not reach $p-1$ (ie $b < p-1$)
Finding the Maximal Subarray: Case 1
- This case ($b = p-1$, ie $a .. b$ is the solution to $1 .. p-1$) is easy:
- If $x_p > 0$, then set $b$ to $p$
- Thus, $a\dots p$ is the solution to $1 .. p$
- If $x_p ≤ 0, a .. b$ does not change
- Thus, $a\dots b$, the solution to $1 .. p-1$ is also the solution to $1 .. p$
Maximal Subarray: Case 2
- This case ($b < p-1$) is harder:
- What is the problem?
- What information would make things easier?
- Think about it some.
Maximal Subarray: Extra Information
- Some additional information makes the problem solvable
- Assume that $c .. d$ is the range of the best solution that ends at $d$
- When $p=d+1$ is considered, what can happen to the $c .. d$
- Consider the values of the sums $S_{ab}$ and $S_{cd}$
Maximal Subarray: Diagram
- Diagram showing ab and cd and p
Maximal Subarray: Solution
- An Ada solution:
maxsub.adb (and prettified)
- A simpler solution, that only finds the max, but not where it is:
function maxsub(A) return int -- return the sum of the maximal subarray
bestsum: array(0..A'last) of int -- Holds solution to each subproblem 1 .. n
bestsum(0) := 0 -- a initial value so we can access bestsum(1-1)
for i in A'range loop
bestsum(i) := A(i) + max(0, bestsum(i-1))
end loop
return max(bestsum)

