Dynamic Programming - Optimal Binary Search Trees
Overview
Optimal Binary Search Trees - Problem
- Problem:
- Sorted set of keys $k_1, k_2, ..., k_n$
- Key probabilities: $p_1, p_2, ..., p_n$
- What tree structure has lowest expected cost?
- Cost of searching for node $i$: $\text{cost}(k_i) = \text{depth}(k_i) + 1$
$
\displaystyle
\begin{align*}
\text{Expected Cost of tree }
& = \sum_{i=1}^n \text{cost}(k_i)p_i \\
& = \sum_{i=1}^n (\text{depth}(k_i) + 1) p_i \\
& = \sum_{i=1}^n \text{depth}(k_i) p_i + \sum_{i=1}^n p_i \\
& = \left(\sum_{i=1}^n \text{depth}(k_i) p_i\right) + 1
\end{align*}
$
Optimal BST - Example
- Example:
- Probability table ($p_i$ is the probabilty of key $k_i$:
| $i$ |
1 |
2 |
3 |
4 |
5 |
| $k_i$ |
$k_1$ |
$k_2$ |
$k_3$ |
$k_4$ |
$k_5$ |
| $p_i$ |
0.25 |
0.20 |
0.05 |
0.20 |
0.30 |
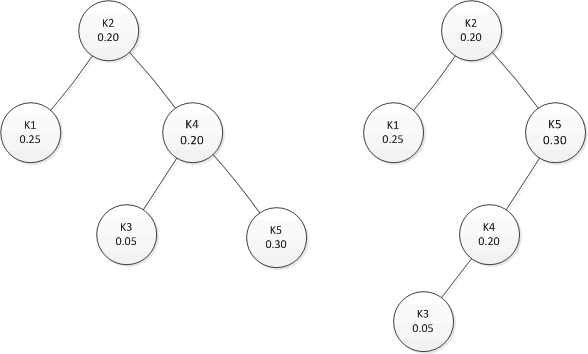 Two BSTs
Two BSTs
- Given: $k_1 < k_2 < k_3 < k_4 < k_5 $
- Tree 1:
- $k_2 / [k_1, k_4] / [nil, nil], [k_3, k_5] $
- cost = 0(0.20) + 1(0.25+0.20) +2(0.05+0.30) + 1 = 1.15 + 1
- Tree 2:
- $k_2 / [k_1, k_5] / [nil, nil], [k_4, nil] /
[nil,nil],[nil,nil], [k_3, nil], [nil,nil] $
- cost = 0(0.20) + 1(0.25+0.30) +2(0.20) + 3(0.05) + 1 = 1.10 + 1
- Notice that a deeper tree has expected lower cost
Optimal BST - DP Approach
- Optimal BST $T$ must have subtree $T'$ for keys $k_i \dots k_j$ which is optimal for those
keys
- Cut and paste proof: if $T'$ not optimal, improving it will improve $T$, a contradiction
- Algorithm for finding optimal tree for sorted, distinct keys $k_i \dots k_j$:
- For each possible root $k_r$ for $i ≤ r ≤ j$
- Make optimal subtree for $k_i, \dots, k_{r-1}$
- Make optimal subtree for $k_r+1, \dots, k_j$
- Select root that gives best total tree
- Formula: $e(i, j)$ = expected number of comparisons for optimal tree for keys
$k_i \dots k_j$
$
\displaystyle
e(i, j) =
\begin{cases}
0, \text{ if } i = j + 1 \\
\min_{i ≤ r ≤ j} \{e(i, r-1) + e(r+1, j) + w(i,j)\}, \text{ if } i ≤ j
\end{cases}
$
- where $\displaystyle w(i, j) = \sum_{k=i}^j p_i$ is the increase in cost if $k_i\dots k_j$ is a subtree of a node
- Work bottom up and remember solution
Optimal BST - Algorithm and Performance
- Brute Force: try all tree configurations
- Ω(4n / n3/2) different BSTs with n nodes
- DP: bottom up with table: for all possible contiguous sequences of keys
and all possible roots, compute optimal subtrees
for size in 1 .. n loop -- All sizes of sequences
for i in 1 .. n-size+1 loop -- All starting points of sequences
j := i + size - 1
e(i, j) := float'max;
for r in i .. j loop -- All roots of sequence ki .. kj
t := e(i, r-1) + e(r+1, j) + w(i, j)
if t < e(i, j) then
e(i, j) := t
root(i, j) := r
end if
end loop
end loop
end loop
Θ(n3)
Can, of course, also use (memoized) recursion
 Two BSTs
Two BSTs