Part 1: Automata and Languages
Chapter 1: Regular Languages
Section 1.1a: Finite Automata and Regular Languages
Part One Goals
- Part One: Automata and Languages
- Automata = Machines
- A language is ... .
- Goal: Learn to use a machine to define a language
Part One Goals - Ways to Define a Language
- List the strings. Examples: ...
- English:
- Example: all binary strings of length 3 or less that start with 1
- Example: all binary strings that start with 1
- Build a machine that tests whether a string is or is not in the language
- Regular Expressions (Section 1.3)
- Grammars (Chapter 2)
Chapter 1 Goals - Language Goals
- Given a language, define a machine that defines that language
- Given a machine, determine the language that it defines
Chapter 1 Tasks
- Learn about finite state machines (aka finite state automata)
- Learn about computation
- Learn about Nondeterminism
- Learn about Regular Languages
- Learn how to test for non-regular languages (ie pumping lemma)
Section Goals
- Use machines to define languages
- Start with simplest machines (finite automata) and languages (regular languages)
- Precisely define Finite Automata/Machine
- Precisely define computation
- Define regular languages
- Define regular operations
- Consider the closure of regular operations
Finite State Machines
Example Finite Automata: Door Controller
- States: Closed, Open
- Inputs: Front, Rear, Both, Neither
- Another view of the inputs - four possible values: {00, 01, 10, 11} or,
equivalently, {0, 1, 2, 3}
- See diagram and table, pages 32, 33
- Machine must specify what to do in each state for each input
- Computation: Machine runs forever, opening and closing
-
Computations are different for machines that operate on strings
Computations Using Strings
- Remember the rules for computation with a FSM:
- Start at start state (ie open-ended arrow)
- Process the string: make one transition for each input character
- Assume input marker is between symbols
- Computation is complete when the end of string is reached
- String is accepted (ie validated) if computation ends in an accept state
(ie double circle)
- Can specify current state at each input point
Examples Revisited
- Example 1: Bit Strings
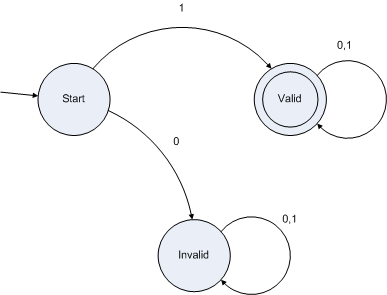
- Example 2: Identifiers
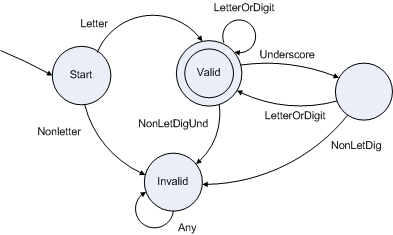
- These machines validate a string as being a bit string that ... or an identifier that ...
Finite Automata: More Examples
- Example 1.7, page 37
- Example 1.9, page 38
- Example 1.11, page 38
- Example 1.13, page 39 (first w/o reset)
- Example 1.15, page 40
- Figure 1.6, page 36
States Provide Limited Memory
- States provide limited memory of what's been seen so far in the input
- Examples 1.7 and 1.9: most recent symbol (2 symbols, 2 states)
- Example 1.11: nothing, first and most recent
- Example: 1.13: sum mod 3 so far
- Current state represents the computation at a given point in the input
Designing Finite Automata
- Start by determine what states are needed
- Specify transition for each input from each state
- Example: recognizing all strings that contain 000
Designing Finite Automata: Examples
- The example languages are over {0, 1} or {a, b}
- L = {w | w does not contain 000}
- L = { w | w ends with two or more a's}}
- L = { w | w ends with one or more b's and does not contain aa}
Precisely Defining a Finite Automata - What to Specify?
- States and their names
- Possible inputs
- Transitions on each input for each state
- Which is the start state
- Which are the accepting states
Finite Automata: Formal Definition
- A finite automata M is a 5-tuple
M = (Q, Σ, δ, q0, F)
where
- Q is a finite set called the states
- Σ is a finite set called the alphabet
- δ: Q × Σ → Q is the transition function
- q0 ∈ Q is the start state
- F ⊆ Q is the set of accept states (aka final states)
- Example: Example 1.11, page 38
- You must memorize this!
Formal Definition and Empty Sets A
- Can Q be empty?
- Can Σ be empty?
- Can δ be empty?
- Can F be empty?
Machine M Recognizes/Accepts a String
- Machine M accepts string w if machine M
ends up in an accept state when it processes w
- We also say that M recognizes w
Machine M Recognizes a Language
Machine M Accepts a Language
L(M) = A
- The Language accepted by M is the set of strings
accepted by M
- We also say that M recognizes Language M
- The set of strings recognized by M is written as L(M)
- Notice that a machine defines a language (ie the one accepted by it)
- Every machine recognizes one language
- If M recognizes no strings, then L(M) = ∅
- You must memorize this!
Computation: Formal Definition of Accepts
- Let
M = ( Q, Σ, δ, q0, F)
be a FSM
- Let w be an input string made up of wi
from Σ, for i in 1 .. n
- Then M accepts w iff there is a sequence of states
r0, r1,
...
rn
such that
- r0 = q0
- δ(ri, wi+1) = ri+1 for i in 0
.. n-1
- rn ∈ F
- Contrast the formal and informal definitions
- You must memorize this!
Regular Language: Definition
- A language is called a Regular Language if some finite
automata recognizes it
- All of the examples recognize regular languages
- Later we will see other ways to define regular languages
Questions on Regular Languages
- How many language(s) per machine
- How many machine(s) per language
- What machines recognize these languages:
- In each case, think about what the following are: Σ, Machine, Language
ITEC 420 Course Page,
Last modified on



