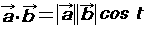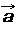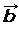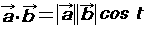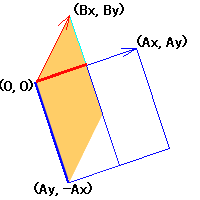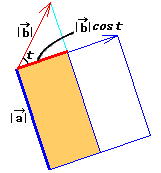
Inner Product(Dot Product)

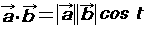
The difinition of Inner Product is . It is represented by the area of the rectangle. If cos t>0,the sign of the area sign is "+",and if cos t<0,then "-".
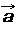
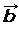
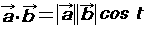
Next, we transform the rectangle into the parallelogram as the right figure without changing the area. Let =(Ax,Ay) and =(Bx,By). The area of the rectangle is equal to the area of the parallelogram created by vector(Ay,-Ax) and (Bx,By).So,the area is AxBx+AyBy. =AxBx+AyBy Please refer to the applet"The Area of a Parallelogram (1)" or "The Area of a Parallelogram (2)".

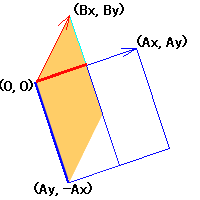
How to use this applet. 1.Press "Next" button to make the rectangle. 2.Check "Motion of the vector" to decide how you move the vectors. 3.Drag red point to move the vectors. 4.Press "transform"button to transform the rectangle into the parallelogram.