The transition probability

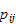 is the probability that if the system is in state
is the probability that if the system is in state

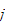 at any one observation, it will be in state
at any one observation, it will be in state

 at the next observation.
at the next observation.
A general model of a system which moves from one state to state is described and applied to concrete problem. It is shown that such systems tend to a steady-state eventually.
The transition probability

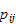 is the probability that if the system is in state
is the probability that if the system is in state

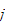 at any one observation, it will be in state
at any one observation, it will be in state

 at the next observation.
at the next observation.
A transition matrix

![$P=[p_{ij}]$](markov__4.png) is any square matrix with nonnegative entries, all of whose column sums are
one.
is any square matrix with nonnegative entries, all of whose column sums are
one.
The probability vectors (column vectors of a transition matrix)

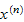 for
for

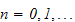 are said to be the state vectors of a Markov process if the
are said to be the state vectors of a Markov process if the

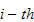 component
component

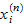 of
of

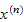 is the probability that the system is in the
is the probability that the system is in the

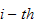 state at the
state at the

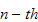 observation.
observation.
If

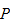 is the transition matrix of a Markov process and
is the transition matrix of a Markov process and

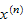 is the state vector at the
is the state vector at the

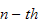 observation, then
observation, then
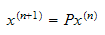
A car rental agency has three rental locations, 1, 2, and 3. A customer may rent a car from any of the three locations and return the car to any of the three locations. The manager finds that the customers return the cars to the various locations according to the following probabilities:

where

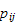 stands for the probability of renting a car from location
stands for the probability of renting a car from location

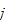 and return it to location
and return it to location

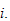 Suppose a car is initially rented from location number 2.
Suppose a car is initially rented from location number 2.
(1) Find the state vector

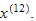
(2) Predict

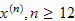 .
.
We define

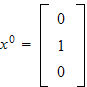 ,
and
,
and

which is designed to compute
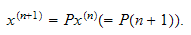
Then

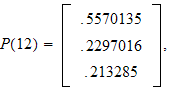

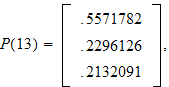

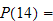

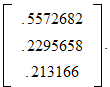 So all state vectors are equal to
So all state vectors are equal to

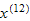 to three decimal places.
to three decimal places.
What if we set

 ? We obtain that
? We obtain that

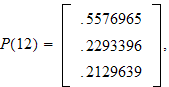

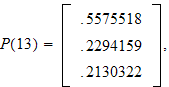 and
and

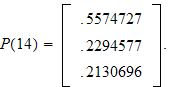
A transition matrix is regular if some integer power of it has all positive entries.
If

 is a regular transition matrix, then as
is a regular transition matrix, then as


where the

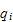 are positive numbers such that
are positive numbers such that

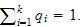
If

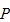 is a regular transition matrix and
is a regular transition matrix and

 is any probability vector, then as
is any probability vector, then as

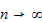
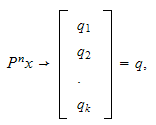
where

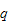 is a fixed probability vector independent of
is a fixed probability vector independent of

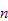 .
.
Note that if

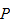 is regular, then as
is regular, then as

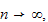 then
then

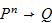 for some
for some

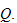 Thus
Thus

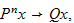 which is a fixed vector and we set it to be
which is a fixed vector and we set it to be

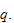
Let

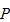 be an transition matrix of a Markov process. State vector
be an transition matrix of a Markov process. State vector

 is called a stable state or steady state of the Markov process if
is called a stable state or steady state of the Markov process if
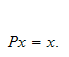
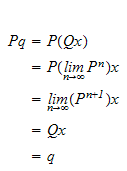
The transition matrix

 .
Find the steady-state vector
.
Find the steady-state vector

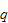 .
.
Method 1: We compute

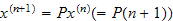 as we did in the previous example.
as we did in the previous example.
Method 2: If

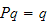 ,
then
,
then

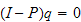 ,
which is equivalent to solve a homogeneous linear system. (We build Identity
matrix with Scientific Workplace by using ''Matrices + Fill Matrix +
Identity''.) We set
,
which is equivalent to solve a homogeneous linear system. (We build Identity
matrix with Scientific Workplace by using ''Matrices + Fill Matrix +
Identity''.) We set

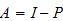 as follows:
as follows:

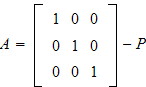

 .
We solve
.
We solve
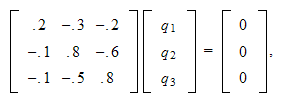
and
the "Solution is :

