Is it true that if
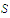 is an unbounded set of real numbers and
is an unbounded set of real numbers and
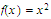 for every number
for every number
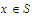 then the function
then the function
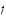 fails to be uniformly continuous?
fails to be uniformly continuous?
The assertion given here is false. Every
function defined on the set
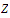 of integers must be uniformly continuous.
of integers must be uniformly continuous.
Given that
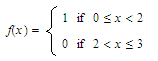 prove
that
prove
that
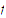 is continuous but not uniformly continuous on the set
is continuous but not uniformly continuous on the set
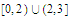 .
.
Since the number
 does not belong to the domain of
does not belong to the domain of
 ,
the function
,
the function
 is constant in a neighborhood of every number in its domain. Therefore
is constant in a neighborhood of every number in its domain. Therefore
 is continuous on the set
is continuous on the set
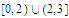 .
To see why
.
To see why
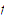 fails to be uniformly continuous we observe that given any positive number
fails to be uniformly continuous we observe that given any positive number
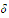 we can find a number
we can find a number
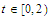 and a number
and a number
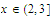 such that
such that
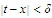 ,
and for any such choice of numbers
,
and for any such choice of numbers
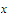 and
and
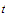 we must
have
we must
have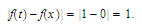
Given that
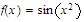 for all real numbers
for all real numbers
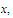 prove that
prove that
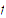 is not uniformly continuous on the set
is not uniformly continuous on the set
 .
.
We
define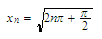 and
and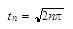 for
every positive integer
for
every positive integer
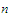 .
Since
.
Since
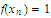 and
and
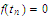 for every
for every
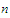 we
know that
we
know that
 does not approach
does not approach
 as
as
 .
Now
.
Now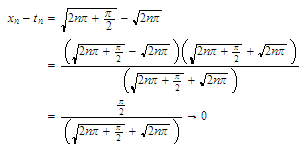 as
as
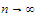 and so it follows from
the
relationship between limits of sequences and uniform continuity that the
function
and so it follows from
the
relationship between limits of sequences and uniform continuity that the
function
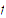 fails to be uniformly continuous.
fails to be uniformly continuous.
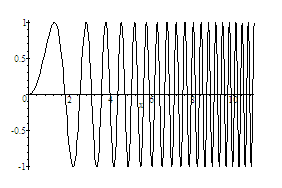
 Ask Scientific Notebook to make some 2D plots of the function
Ask Scientific Notebook to make some 2D plots of the function
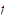 defined by the equation
defined by the equation
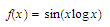 for
for
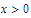 .
Plot the function on each of the intervals
.
Plot the function on each of the intervals
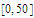 ,
,
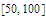 ,
,
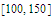 and
and
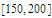 .
Revise your plot and increase its sample size if it appears to contain errors.
Why do these graphs suggest that
.
Revise your plot and increase its sample size if it appears to contain errors.
Why do these graphs suggest that
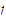 fails to be unformly continuous on the interval
fails to be unformly continuous on the interval
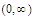 ?
Prove that this function does, indeed, fail to be uniformly continuous.
?
Prove that this function does, indeed, fail to be uniformly continuous.
Solution: To prove that
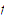 fails
to be uniformly continuous we shall show that for every number
fails
to be uniformly continuous we shall show that for every number
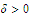 there
exist two positive numbers
there
exist two positive numbers
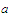 and
and
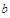 such
that
such
that
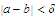 and
and
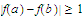 .
We begin by choosing a number
.
We begin by choosing a number
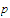 such
that whenever
such
that whenever
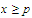 we
have
we
have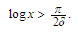 Now
choose a positive integer
Now
choose a positive integer
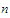 such
that
such
that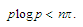 Since
Since
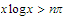 for
for
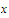 sufficiently
large
sufficiently
large
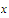 ,
we can use the Bolzano intermediate value theorem to choose a number
,
we can use the Bolzano intermediate value theorem to choose a number
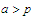 such
that
such
that
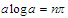 .
Now since
.
Now since
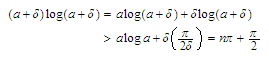 we
can use the Bolzano intermediate value theorem again to choose a number
we
can use the Bolzano intermediate value theorem again to choose a number
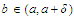 such
that
such
that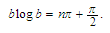 We
now observe
that
We
now observe
that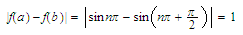 and
so the proof is complete.
and
so the proof is complete.
-
A function
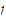 is said to be Lipschitzian on a set
is said to be Lipschitzian on a set
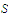 if there exists a number
if there exists a number
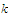 such that the inequality
such that the inequality
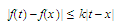 holds
for all numbers
holds
for all numbers
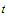 and
and
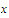 in
in
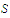 .
Prove that every Lipschitzian function is uniformly continuous.
.
Prove that every Lipschitzian function is uniformly continuous.
Suppose that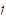 is a function defined on a set
is a function defined on a set
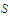 ,
that
,
that
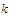 is a positive number and that the
inequality
is a positive number and that the
inequality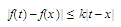 holds
for all numbers
holds
for all numbers
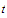 and
and
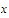 in the set
in the set
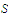 .
Suppose that
.
Suppose that
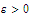 .
We define
.
We define
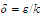 and
observe that, whenever
and
observe that, whenever
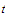 and
and
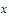 belong to
belong to
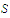 and
and
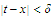 we
have
we
have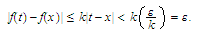
-
Given that
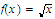 for all
for all
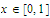 prove that
prove that
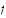 is uniformly continuous but not lipschitzian on
is uniformly continuous but not lipschitzian on
![$\left[ 0,1\right] $](graphics/Uniform Continuity-hint__93.png) .
.
Solution: The fact that
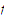 is
uniformly continuous on the closed bounded set
is
uniformly continuous on the closed bounded set
![$\left[ 0,1\right] $](graphics/Uniform Continuity-hint__95.png) follows
at once from the fact that
follows
at once from the fact that
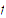 is
continuous there. Now, to prove that
is
continuous there. Now, to prove that
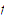 fails
to be Lipschitzian, suppose that
fails
to be Lipschitzian, suppose that
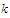 is
any positive number. Given
is
any positive number. Given
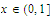 we
see
that
we
see
that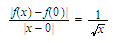 and
this exceeds
and
this exceeds
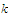 whenever
whenever
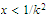 .
.
-
Suppose that
 is uniformly continuous on a set
is uniformly continuous on a set
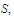 that
that
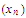 is a sequence in the set
is a sequence in the set
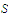 and that
and that
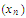 has a partial limit
has a partial limit
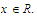 Prove that it is impossible to have
Prove that it is impossible to have
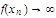 as
as
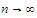 .
.
Using the fact that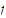 is uniformly continuous on
is uniformly continuous on
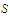 we choose a number
we choose a number
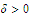 such that the inequality
such that the inequality
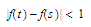 holds
whenever
holds
whenever
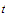 and
and
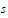 belong to
belong to
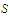 and
and
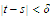 .
Since
.
Since
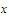 is a partial limit of the sequence
is a partial limit of the sequence
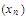 we know that the
condition
we know that the
condition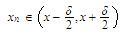 holds
for infinitely many positive integers
holds
for infinitely many positive integers
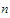 .
Choose a positive integer
.
Choose a positive integer
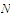 such
that
such
that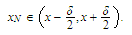 For
every one of the infinitely many positive integers
For
every one of the infinitely many positive integers
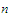 for which the
condition
for which the
condition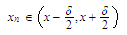 holds,
since
holds,
since
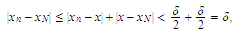 we
have
we
have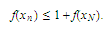 Therefore
the sequence of numbers
Therefore
the sequence of numbers
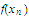 is frequently in the interval
is frequently in the interval
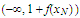 and so it cannot approach
and so it cannot approach
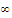 .
.
Of course, this sequence cannot approach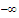 either.
either.
-
Did you assume that
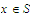 in Part a? If you did, go back and do the exercise again. You have no
information that
in Part a? If you did, go back and do the exercise again. You have no
information that
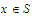 .
If you didn't assume
.
If you didn't assume
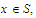 you can sit this question out.
you can sit this question out.
-
Suppose that
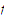 is uniformly continuous on a bounded set
is uniformly continuous on a bounded set
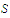 and that
and that
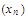 is a sequence in
is a sequence in
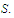 Prove that it is impossible to have
Prove that it is impossible to have
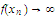 as
as
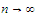 .
.
The assertion follows at once from Part a and the fact that every bounded sequence of numbers has a partial limit in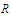 .
.
-
Prove that if
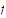 is uniformly continuous on a bounded set
is uniformly continuous on a bounded set
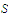 then the function
then the function
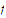 is bounded.
is bounded.
Solution: To obtain a contradiction, assume that
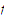 is
unbounded above. Choose a sequence
is
unbounded above. Choose a sequence
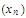 in
in
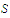 such
that
such
that
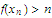 for
each
for
each
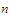 .
Now use part c of this exercise.
.
Now use part c of this exercise.
Well, of course, such a choice of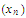 would make
would make
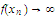 which we know now to be impossible.
which we know now to be impossible.
-
Given that
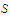 is a set of real numbers, that
is a set of real numbers, that
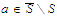 and that
and that
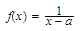 for
all
for
all
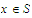 ,
prove that
,
prove that
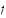 is continuous on
is continuous on
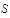 but not uniformly continuous.
but not uniformly continuous.
Hint: Use the preceding exercise. Choose a sequence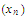 in
in
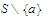 that
converges to
that
converges to
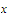 .
Note that
.
Note that
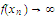 as
as
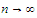 .
.
-
Given that
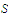 is a set of real numbers and that
is a set of real numbers and that
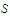 fails to be closed, prove that there exists a continuous function on
fails to be closed, prove that there exists a continuous function on
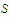 that fails to be uniformly continuous on
that fails to be uniformly continuous on
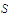 .
.
Choose a number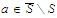 and use Part a.
and use Part a.
-
Is it true that if
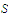 is an unbounded set of real numbers then there exists a continuous function on
is an unbounded set of real numbers then there exists a continuous function on
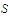 that fails to be uniformly continuous on
that fails to be uniformly continuous on
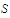 ?
?
No, as we remarked after Exercise 1, every function on the set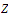 of integers must be uniformly continuous.
of integers must be uniformly continuous.
Is it true that the composition of a uniformly continuous function with a
uniformly continuous function is uniformly continuous?
Yes, this assertion
is true. Suppose that
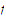 is a uniformly continuous function on a set
is a uniformly continuous function on a set
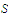 and that
and that
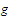 is a uniformly continuous function on a set
is a uniformly continuous function on a set
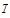 that includes the range
that includes the range
![$f\left[ S\right] $](graphics/Uniform Continuity-hint__177.png) of
of
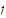 .
To show that the function
.
To show that the function
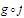 is uniformly continuous on
is uniformly continuous on
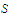 ,
suppose that
,
suppose that
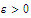 .
.
Using the uniform continuity of
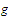 on the set
on the set
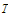 we choose a number
we choose a number
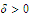 such that the inequality
such that the inequality
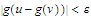 holds whenever
holds whenever
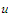 and
and
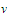 belong to
belong to
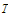 and
and
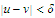 .
Now, using the uniform continuity of
.
Now, using the uniform continuity of
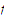 on the set
on the set
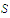 we choose a positive number
we choose a positive number
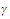 such that the inequality
such that the inequality
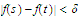 will hold whenever
will hold whenever
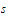 and
and
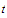 belong to
belong to
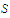 and
and
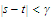 .
Then whenever
.
Then whenever
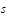 and
and
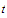 belong to
belong to
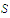 and
and
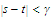 we
have
we
have
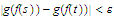 .
.
-
Suppose that
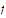 is uniformly continuous on a set
is uniformly continuous on a set
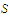 and that
and that
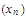 is a convergent sequence in
is a convergent sequence in
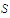 .
Prove that the sequence
.
Prove that the sequence
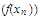 cannot have more than one partial limit.
cannot have more than one partial limit.
We know from the result proved in Exercise 6 d that the sequence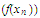 is bounded. We choose a partial limit
is bounded. We choose a partial limit
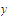 of
of
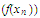 and we want to prove that
and we want to prove that
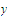 is the only partial limit of
is the only partial limit of
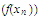 .
Suppose that
.
Suppose that
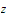 is any number unequal to
is any number unequal to
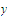 .
We define
.
We define
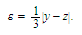 Choose
a number
Choose
a number
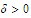 such that the
inequality
such that the
inequality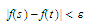 holds
whenever
holds
whenever
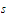 and
and
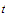 belong to
belong to
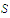 and
and
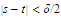 .
.
We write the limit of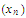 as
as
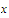 and choose an integer
and choose an integer
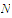 such that the inequality
such that the inequality
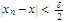 holds whenever
holds whenever
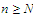 .
Using the fact that
.
Using the fact that
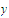 is a partial limit of the sequence
is a partial limit of the sequence
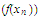 we choose an integer
we choose an integer
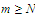 such that
such that
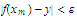 .
Now given any integer
.
Now given any integer
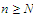 ,
since
,
since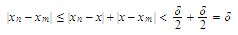 we
must
have
we
must
have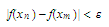 and
consequently
and
consequently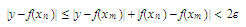

Thus if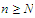 ,
the number
,
the number
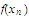 cannot lie in the neighborhood
cannot lie in the neighborhood
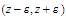 of
of
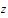 and we conclude that
and we conclude that
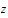 fails to be a partial limit of the sequence
fails to be a partial limit of the sequence
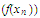 .
.
-
In Part a, did you assume that the limit of the sequence
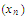 belongs to
belongs to
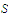 ?
If so, go back and do the problem again.
?
If so, go back and do the problem again.
-
Prove that if
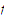 is uniformly continuous on a set
is uniformly continuous on a set
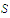 and
and
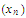 is a convergent sequence in
is a convergent sequence in
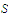 then the sequence
then the sequence
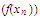 is also convergent. Do not assume that the limit of
is also convergent. Do not assume that the limit of
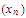 belongs to
belongs to
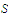 .
.
In view of Part a, the present result follows at once from an earlier theorem on limits of sequences. -
Suppose that
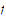 is uniformly continuous on a set
is uniformly continuous on a set
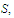 that
that
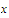 is a real number and that
is a real number and that
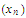 and
and
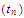 are sequences in
are sequences in
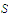 that converge to the number
that converge to the number
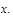 Prove that
Prove that
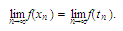 The
existence of these limits was guaranteed in Part c. Now since
The
existence of these limits was guaranteed in Part c. Now since
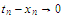 as
as
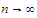 we deduce from
the
relationship between uniform continuity and limits of sequences that
we deduce from
the
relationship between uniform continuity and limits of sequences that
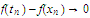 as
as
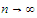 .
.
-
Suppose that
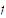 is uniformly continuous on a set
is uniformly continuous on a set
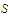 and that
and that
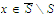 .
Explain how we can use Part d to extend the definition of the function
.
Explain how we can use Part d to extend the definition of the function
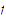 to the number
to the number
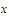 in such a way that
in such a way that
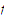 is continuous on the set
is continuous on the set
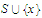 .
.
We know that there exists a sequence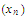 in
in
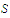 that converges to
that converges to
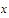 and
we know that there is a single limit for all of the sequences
and
we know that there is a single limit for all of the sequences
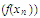 that can be made in this way. We define
that can be made in this way. We define
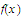 to be this common limit value. This extension of the function
to be this common limit value. This extension of the function
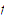 to the set
to the set
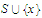 is uniformly continuous. The proof will be given in the more extended case
that we consider below in Part f.
is uniformly continuous. The proof will be given in the more extended case
that we consider below in Part f.
-
Prove that if
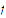 is uniformly continuous on a set
is uniformly continuous on a set
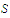 then it is possible to extend
then it is possible to extend
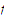 to the closure
to the closure
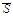 of
of
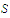 in such a way that
in such a way that
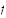 is uniformly continuous on
is uniformly continuous on
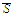 .
.
For every number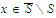 we define
we define
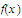 by the method described in Part e. To show that the extension of
by the method described in Part e. To show that the extension of
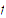 to
to
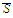 is uniformly continuous, suppose that
is uniformly continuous, suppose that
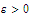 .
Using the uniform continuity of
.
Using the uniform continuity of
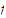 on
on
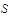 we choose
we choose
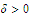 such that the inequality
such that the inequality
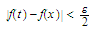 holds
whenever
holds
whenever
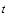 and
and
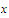 belong to
belong to
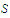 and
and
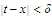 .
We shall now observe that whenever
.
We shall now observe that whenever
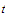 and
and
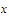 belong to
belong to
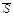 and
and
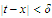 we must have
we must have
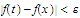 .
To make this observation, suppose that
.
To make this observation, suppose that
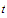 and
and
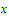 belong to
belong to
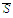 and that
and that
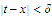 .
.
choose a sequence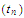 in
in
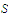 that converges to
that converges to
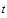 and a sequence
and a sequence
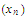 in
in
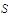 that converges to
that converges to
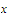 .
Since
.
Since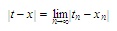 we
know that the inequality
we
know that the inequality
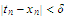 must hold for all
must hold for all
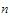 sufficiently large and therefore,
since
sufficiently large and therefore,
since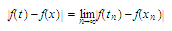 and
since
and
since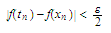 for
all
for
all
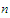 sufficiently large we must
have
sufficiently large we must
have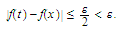
Suppose that
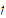 is a continuous function on a bounded set
is a continuous function on a bounded set
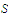 .
rove that the following two conditions are equivalent:
.
rove that the following two conditions are equivalent:
-
The function
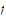 is uniformly continuous on
is uniformly continuous on
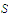 .
.
-
It is possible to extend
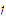 to a continuous function on the set
to a continuous function on the set
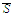 .
.
The fact that condition a implies condition b follows from Exercise 9. On the
other hand, if
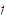 has a continuous extension to the set
has a continuous extension to the set
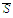 then, this extension, being a continuous function on a closed bounded set,
must be uniformly continuous; and so
then, this extension, being a continuous function on a closed bounded set,
must be uniformly continuous; and so
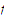 must be uniformly continuous on
must be uniformly continuous on
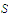 .
.
Given that
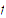 is a function defined on a set
is a function defined on a set
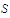 of real numbers, prove that the following conditions are equivalent:
of real numbers, prove that the following conditions are equivalent:
-
The function
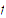 fails to be uniformly continuous on the set
fails to be uniformly continuous on the set
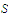 .
.
-
There exists a number
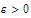 and there exist two sequences
and there exist two sequences
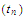 and
and
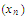 in
in
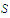 such that
such that
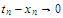 as
as
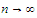 and
and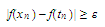 for
every
for
every
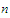 .
.
At the suggestion of my good friend Sean Ellermeyer this exercise was upgraded to a theorem. I have left in the exercise. Sometimes I find it interesting to see which of my students recognize that an item is the same as one they have already seen.