If
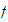 is continuous on
is continuous on
![$[a,b]$](http://www.radford.edu/~wyang/430/converseMVT/graphics/converse-MVTweb__2.png) and differentiable on
and differentiable on
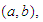 then
there is a point
then
there is a point
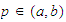 such that
such that
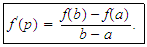
Dr. Wei-Chi Yang
Radford University
Radford, VA 24142
www.radford.edu/~wyang
If
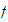 is continuous on
is continuous on
![$[a,b]$](http://www.radford.edu/~wyang/430/converseMVT/graphics/converse-MVTweb__2.png) and differentiable on
and differentiable on
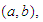 then
there is a point
then
there is a point
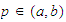 such that
such that
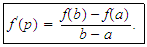
Conversely, we can ask under what condition, for all
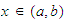 there is a
there is a
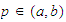 such that
such that
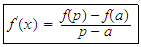 or
or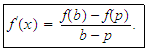
Suppose
f is strictly monotone in the interval
is strictly monotone in the interval
![$[a,b].$](http://www.radford.edu/~wyang/430/converseMVT/graphics/converse-MVTweb__11.png) Then there exists
Then there exists
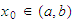 such that
such that
When
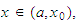 there exists a unique
there exists a unique
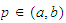 satisfying
satisfying
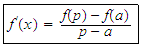
When
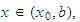 there exists a unique
there exists a unique
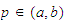 satisfying
satisfying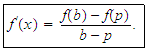 Remark:
For CP,
click here.
Remark:
For CP,
click here.