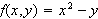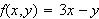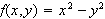Review the followings if

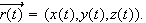
-
the arc length of

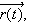
-
the unit tangent vector,

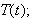
-
the unit normal vector,

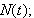
-
the unit binormal vector,

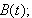
-
the curvature function, (theorem 9,10 and 11)
-
the velocity function,
-
the acceleration function.
-
express the acceleration function in terms of

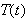 and
and

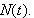
Consider the space curve

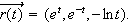
-
Find the tangent line when

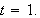
-
Set up the integral for the arc length of

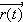 for
for

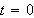 to
to

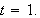
-
Use Maple to figure out

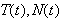 and
and

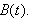
Repeat problem 2 above if

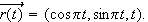
Consider the space curve

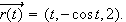
-
Sketch the curve from

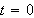 to
to

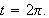
-
Draw the vectors

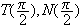 and
and

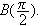
-
Indicate where the curvature for

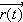 is the largest and the smallest (by inspection) for
is the largest and the smallest (by inspection) for

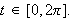
Use implicit differentiation to find the curvature of an ellipse

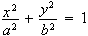 at
at

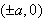 and
and

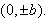
Understanding the contour map and the level curves. For example:
The existence of a limit

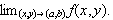
-
Review examples from your notes and homeworks.
-
Determine if

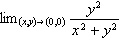 exists.
exists.
-
Find the limit if it exists:

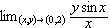
Find the region where

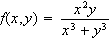 is continuous.
is continuous.
Find the region where

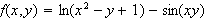 is continuous.
is continuous.
Understanding Partial Derivatives algebraically and graphically.
-
Consider

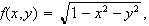
-
find

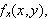
-
If

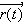 is the curve traveling traveling along
is the curve traveling traveling along

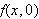 from
from

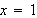 to
to

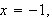 find the parameterization for
find the parameterization for

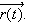
-
explain the relationship between

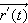 and
and

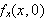
-
-
Try the homworks from the text.
-
Use Maple to understand partial derivatives graphically.