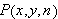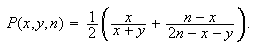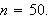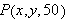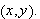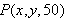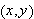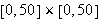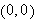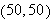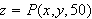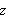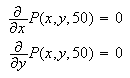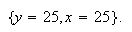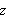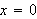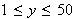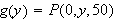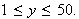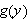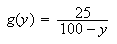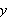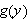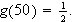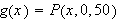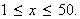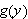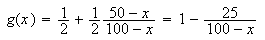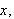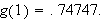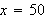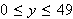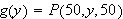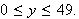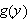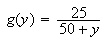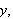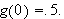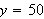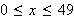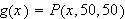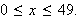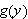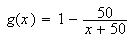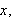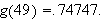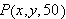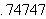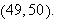Maximizing a Probability Function
Extracted from the book "Exploring Mathmematics with Scientific Notebook",
Published by Springer Verlag, ISBN #981-3083-88-3, by me and Professor
Jonathan Lewin of Kennesaw State University, Georgia.
In this example, we suppose that we have

 white balls and
white balls and

 black balls which we are going to place in two urns A and B in any way we
please, as long as at least one ball is placed into each urn. After this has
been done, a second person walks into the room and selects one ball at random.
Our problem is to maximize the probability that this person draws a white
ball.
black balls which we are going to place in two urns A and B in any way we
please, as long as at least one ball is placed into each urn. After this has
been done, a second person walks into the room and selects one ball at random.
Our problem is to maximize the probability that this person draws a white
ball.
We suppose that the distribution of the balls in the urns A and B is as
described in the following table:

If

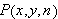 is the probability that a single ball drawn at random will be white then
is the probability that a single ball drawn at random will be white then
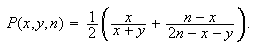
From now on we shall assume that

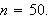 We begin our study of the function by looking at the following table which
shows the values of
We begin our study of the function by looking at the following table which
shows the values of

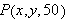 at a few selected points
at a few selected points

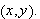

To solve the problem we need to find the maximum value of the expression

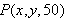 as the point
as the point

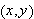 varies through the rectangle
varies through the rectangle

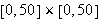 from which the points
from which the points

 and
and

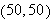 have been removed. If we sketch the graph
have been removed. If we sketch the graph

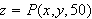 then we obtain the following surface:
then we obtain the following surface:
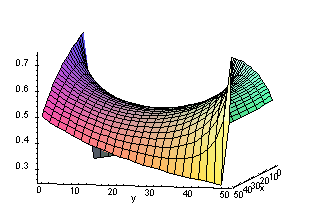
From the looks of this surface it seems unlikely that the maximum value of

 will be achieved at a critical point. The maximum appears to be at the left or
right extremities of the figure. As a matter of fact, if we point at the
equations
will be achieved at a critical point. The maximum appears to be at the left or
right extremities of the figure. As a matter of fact, if we point at the
equations
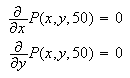
and click on Solve and Exact
then we obtain
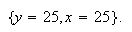
As we have already seen, the maximum value of

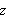 does not occur at the point
does not occur at the point

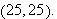
We now examine the boundary behavior of the function. There are four cases to
consider
The Case

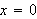 and
and 
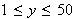
We define

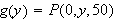 for
for

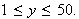 Point at this definition of
Point at this definition of

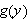 and click on Define and New
Definition. Since
and click on Define and New
Definition. Since
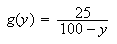
for each

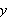 we see that the maximum value of
we see that the maximum value of

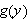 is
is

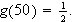
The Case

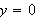 and
and 
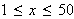
We define

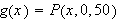 for
for

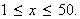 Point at this definition of
Point at this definition of

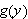 and click on Define and New
Definition. Since
and click on Define and New
Definition. Since
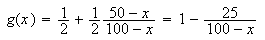
for each

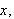 we see that the maximum value of this function is
we see that the maximum value of this function is

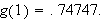
The Case

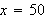 and
and 
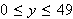
We define

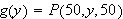 for
for

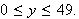 Point at this definition of
Point at this definition of

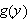 and click on Define and New
Definition. Since
and click on Define and New
Definition. Since
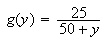
for each

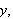 we see that the maximum value of this function is
we see that the maximum value of this function is

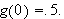
The Case

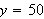 and
and 
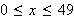
We define

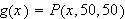 for
for

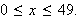 Point at this definition of
Point at this definition of

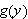 and click on Define and New
Definition. Since
and click on Define and New
Definition. Since
for each

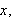 we see that the maximum value of this function is
we see that the maximum value of this function is

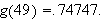
Conclusion
We conclude that the expression

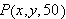 takes a maximum value of
takes a maximum value of

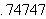 at the point
at the point

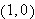 and again at the point
and again at the point

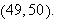 This means that we can maximize the probability that a white ball will be
selected by placing one white ball and no black ball in urn A and all the
other balls in urn B. Alternatively we can place one white ball and just no
black ball in urn B and all the other balls in urn A.
This means that we can maximize the probability that a white ball will be
selected by placing one white ball and no black ball in urn A and all the
other balls in urn B. Alternatively we can place one white ball and just no
black ball in urn B and all the other balls in urn A.
This document created by Scientific WorkPlace 4.0.

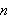 white balls and
white balls and

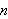 black balls which we are going to place in two urns A and B in any way we
please, as long as at least one ball is placed into each urn. After this has
been done, a second person walks into the room and selects one ball at random.
Our problem is to maximize the probability that this person draws a white
ball.
black balls which we are going to place in two urns A and B in any way we
please, as long as at least one ball is placed into each urn. After this has
been done, a second person walks into the room and selects one ball at random.
Our problem is to maximize the probability that this person draws a white
ball.