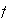 at a point
at a point
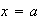 is defined to be
is defined to be
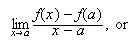
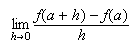
Math 151 Test 2 Print Name Time: 9, 10, 12
Recall that the slope of the tangent line for
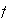 at a point
at a point
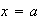 is defined to be
is defined to be
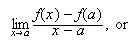
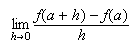
If
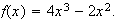
Use the definition to find the slope of the tangent line at
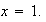
Find the tangent line equation at
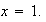
Consider
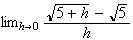 , interpret it as the slope of the tangent line for a function at a point. You
need to identify the function and the point.
, interpret it as the slope of the tangent line for a function at a point. You
need to identify the function and the point.
If
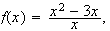
find
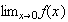 by showing your work,
by showing your work,
determine if
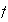 is continuus at
is continuus at
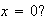 explain.
explain.
sketch the graph of
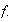
If
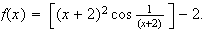 Then
use the squeezing principle to find the limit of
Then
use the squeezing principle to find the limit of
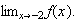 [Specify two functions when applying the squeezing principle.]
[Specify two functions when applying the squeezing principle.]
Let
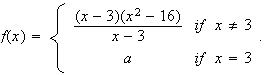
Determine the value
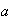 so that the function
so that the function
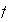 is continuous everywhere.
is continuous everywhere.
Sketch the function
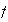 after you find your answer for the number
after you find your answer for the number
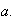
Define a function
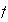 ,
whose graph is similar to the function,
,
whose graph is similar to the function,
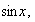 and satisfies ALL the following conditions:
and satisfies ALL the following conditions:
the period of
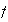 is
is
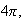
the function
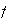 has amplitude of
has amplitude of
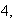
the function
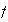 has a maximum at
has a maximum at
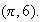
Explain why
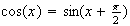 graphically.
graphically.