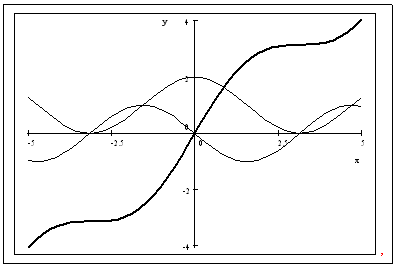
If the graph of
 is given together with its first and second derivatives below. Label the
graphs for
is given together with its first and second derivatives below. Label the
graphs for
 and
and

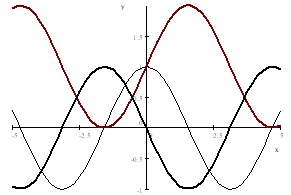
Ans:
 is red,
is red,
 is
thin and
is
thin and
 is
black thick.
is
black thick.
If the graph of
 is given below:
is given below:
-
Compare

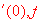
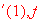
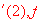
 in increasing order. [ Ans:
in increasing order. [ Ans:
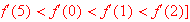
-
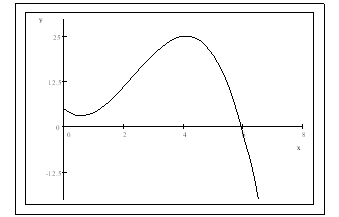
Suppose the function
 (graph of
(graph of
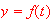 ,
is given above) represent the distance that a car travels.
,
is given above) represent the distance that a car travels.
-
When do you think the car has zero velocity between
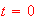 and
and
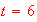 ?
[Ans: look for the point where
?
[Ans: look for the point where
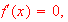 so
it is about
x=4 (max of f) or
x=0.8 (min of f ].
so
it is about
x=4 (max of f) or
x=0.8 (min of f ]. -
Approximate the time when the car reaches its highest speed for
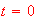 and
and
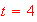 .
[Note: speed =
.
[Note: speed =
 ].
].
[Ans: We look for the slope of
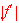 to be the largest, so it is the inflection point of
to be the largest, so it is the inflection point of
 .]
.]
-
Find the tangent line equations and the
 at a given point for the following functions:
at a given point for the following functions:
-
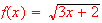 at
at
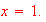 [Ans:
y=0.6708 x+1.565]
[Ans:
y=0.6708 x+1.565]
-
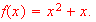 at
at
 [y=-3*x-4]
[y=-3*x-4]
Find
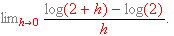 [Hint:
Identify a function
[Hint:
Identify a function
 and a point
and a point
 and use the derivative at one point.]
and use the derivative at one point.]
[Ans. This limit is the same as
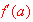 when we pick
when we pick
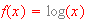 and
and
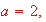 so
it is
so
it is
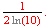 ]
]
Find the following limits with explanations:
-
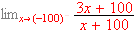 [ans.
[ans.
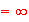 ]
]
-
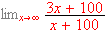 [
[
-
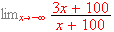 [
[
-
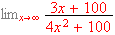 [=0
[=0
-
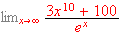 [=0
[=0
-
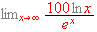 [=0
[=0
Let the graph of a velocity function (x = time, y = feet/sec) be given below:
Assuming the x-intercepts for the following graph is at
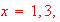 and
and

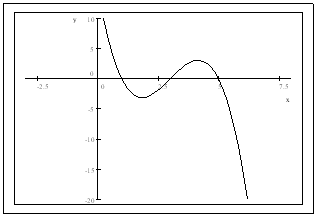
-
What is the initial velocity (when time=0)? [Ans: Since when
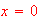 ,
,
 is not found, so we do not have enough info to find the initial velocity.]
is not found, so we do not have enough info to find the initial velocity.]
-
Explain how velocity function can be negative sometimes. [Ans. When we travel in opposite direction, the velocity is negative.]
-
Estimate the inflection point(s) for the distance function
 [Ans,
they are at the local min and the local max of the velocity, so it about
[Ans,
they are at the local min and the local max of the velocity, so it about
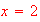 and
and
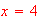 ].
].
-
Estimate the maximum and minimum for the distance function
 [Ans,
max is at
[Ans,
max is at
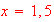 and minimum at
and minimum at
![$x=3.]$](graphics/finalreview__60.png)
-
Find the interval(s) where the acceleration is negative. [Ans. This is where the velocity has negative slopes].
If the graphs of
 and
and
 are given below: Then
are given below: Then
-
identify the graph for
 and
and
 respectively. [Ans.
respectively. [Ans.
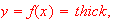
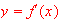 is the one always positive and the last one is for
is the one always positive and the last one is for
 ]
]
-
find the interval(s) where
 is increasing or decreasing, [ans.
is increasing or decreasing, [ans.
 is always increasing]
is always increasing]
-
find the maximum and minimum for
 in the interval
in the interval
![$[0,2\pi ],$](graphics/finalreview__71.png) [since
[since
 is increasing in
is increasing in
![$[0,2\pi ],$](graphics/finalreview__73.png) the minimum is at
the minimum is at
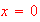 and the maximum is at
and the maximum is at
![$x=2\pi .]$](graphics/finalreview__75.png)
-
find the interval(s) where
 is concave upward and concave downward. [Since
is concave upward and concave downward. [Since
 in
in
 ,
,
 is concave in this interval;similarly,
is concave in this interval;similarly,
 in
in
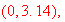
 is concave down this interval.]
is concave down this interval.]
Find the first derivative for the following functions:
-
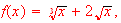 [
[
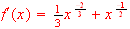
-
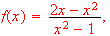 [
[
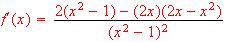
-
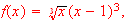 [
[
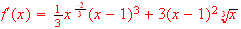
-
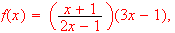 [done
in class]
[done
in class]
-
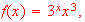 [
[
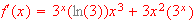
-
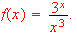 [
[
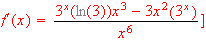
If the derivative of a function is
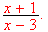 Then
Then
-
find the interval(s) where original function
 is increasing and decreasing, [hint: draw
is increasing and decreasing, [hint: draw
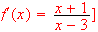
-
find the interval(s) where the original function
 is concave upward and concave downward. [hint: find
is concave upward and concave downward. [hint: find
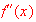 and use the signs of
and use the signs of
 to find the intervals where
to find the intervals where
 is concave upward or downward]
is concave upward or downward]
-
graph one possible function
 which has the derivate function
which has the derivate function
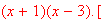 **this
is a typo, ignore this one]
**this
is a typo, ignore this one]
Find
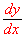 if
if
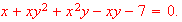 [Use
implicit differentiation to find
[Use
implicit differentiation to find
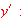
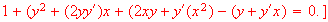
Find
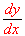 if
if
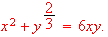 [
[
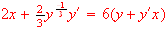 ].
].
Find
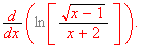 [
[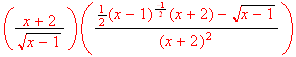
Find the first derivative for the following functions:
-
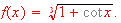 [
[

-
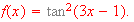 [
[
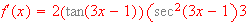
Use the product or quotient rule to find
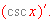
Find the followings:
-
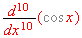 [
[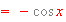
-
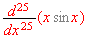 [
[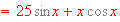
If
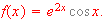 Find
Find
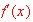 by hand.
by hand.
Suppose the cost, in dollars, for a company to produce
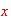 pairs of a new line of jeans
is
pairs of a new line of jeans
is
-
Find the marginal cost function. [
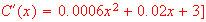
-
Find
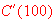 and explain its meaning. What does it predict? [This will predict the cost for
the 101st unit]
and explain its meaning. What does it predict? [This will predict the cost for
the 101st unit]
-
Estimate the cost of making the 99 th pair of jeans. [Use
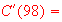 use calculator to find this value]
use calculator to find this value]
If
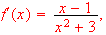
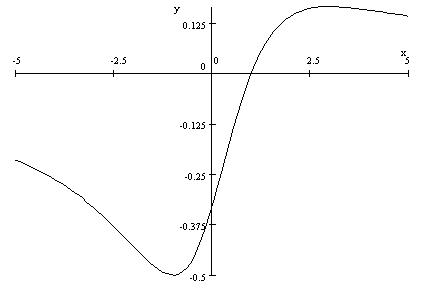
-
use the signs of

 to
find the intervals where
to
find the intervals where
 is increasing or decreasing, [hint: plot
is increasing or decreasing, [hint: plot
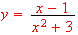 ,
which is shown above. We need find the zero of
,
which is shown above. We need find the zero of
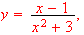 which
is at
which
is at
 so
so
 is increasing in
is increasing in
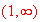 and
and
 is decreasing in
is decreasing in
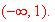 ]
]
-
find the relative maximum and minimum for
 [
[
 has a relative minimum at
has a relative minimum at
![$x=1]$](graphics/finalreview__144.png)
-
find
 [hint:
[hint:
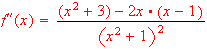
-
use the signs of
 to find the intervals where
to find the intervals where
 is concave upward or downward. [hint: after finding
is concave upward or downward. [hint: after finding
 you need to plot
you need to plot
