Define a function

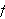 ,
whose graph is similar to the cosine function,
,
whose graph is similar to the cosine function,

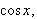 and satisfies ALL the following conditions:
and satisfies ALL the following conditions:
-
the period of

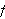 is
is

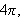
-
the function

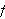 has amplitude of
has amplitude of

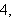
-
the function

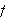 has a maximum value of
has a maximum value of

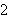 when
when

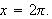 [hint:
You need to come up with ONE function that satisfies All the conditions (a),
(b), and (c); think of changing the period, amplitude, reflection, and
shifting of
[hint:
You need to come up with ONE function that satisfies All the conditions (a),
(b), and (c); think of changing the period, amplitude, reflection, and
shifting of

![$y=\cos x.]$](extracredit__10.png)
[hint: y=-4cos((1/2)*x)-2].
Explain why

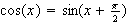 graphically. [because if you shift y=sin(x) to the left pi/2 units,
you will get y=cos(x)]
graphically. [because if you shift y=sin(x) to the left pi/2 units,
you will get y=cos(x)]
Express

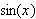 in terms of
in terms of

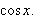
If

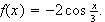
-
Find the period of

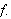 [**the period is 2*pi divides by (1/3) so it is 6*pi].
[**the period is 2*pi divides by (1/3) so it is 6*pi]. -
Find the asymptotes for

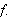 [**a typo here, it is supposed to be amplitude, the amplitude is 2].
[**a typo here, it is supposed to be amplitude, the amplitude is 2]. -
Sketch

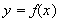
-
Explain the relationship between the graphs of

 and
and

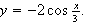 [hint:
[hint: 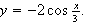 is
being reflected along x-axis from
is
being reflected along x-axis from  and change the amplitude from 1 to 2 and the period of
and change the amplitude from 1 to 2 and the period of 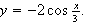 is
6*pi.
is
6*pi.
Find the function whose graph is the reflection of

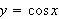 along the
along the

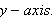 [hint: y=cos(-x)]
[hint: y=cos(-x)]
Find the function whose graph is the reflection of

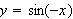 along the
along the

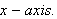 [hint: y=-sin(-x)].
[hint: y=-sin(-x)].