Graphs - Terminology and Representation

Overview

• Definitions: Vertices, edges, paths, etc
• Representations: Adjacency list and adjacency matrix

Definitions: Graph, Vertices, Edges

• Define a graph G = (V, E) by defining a pair of sets:
  1. V = a set of vertices
  2. E = a set of edges
  
  
• Edges:
• Each edge is defined by a pair of vertices
• An edge connects the vertices that define it
• In some cases, the vertices can be the same


• Vertices:
• Vertices also called nodes
• Denote vertices with labels


• Representation:
• Represent vertices with circles, perhaps containing a label
• Represent edges with lines between circles


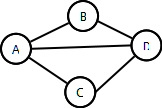
• Example:
• V = {A,B,C,D}
• E = {(A,B),(A,C),(A,D),(B,D),(C,D)}

Motivation

• Many algorithms use a graph representation to represent data or the problem to be solved


• Examples:
• Cities with distances between
• Roads with distances between intersection points
• Course prerequisites
• Network
• Social networks
• Program call graph and variable dependency graph

Graph Classifications

• There are seveal common kinds of graphs
• Weighted or unweighted
• Directed or undirected
• Cyclic or acyclic


• Choose the kind required for problem and determined by data


• We examine each below

Kinds of Graphs: Weighted and Unweighted

• Graphs can be classified by whether or not their edges have weights


• Weighted graph: edges have a weight


• Weight typically shows cost of traversing
• Example: weights are distances between cities


• Unweighted graph: edges have no weight


• Edges simply show connections
• Example: course prereqs

Kinds of Graphs: Directed and Undirected

• Graphs can be classified by whether or their edges are have direction


• Undirected Graphs: each edge can be traversed in either direction


• Directed Graphs: each edge can be traversed only in a specified direction

Undirected Graphs

• Undirected Graph: no implied direction on edge between nodes


• The example from above is an undirected graph



• In diagrams, edges have no direction (ie they are not arrows)


• Can traverse edges in either directions


• In an undirected graph, an edge is an unordered pair


• Actually, an edge is a set of 2 nodes, but for simplicity we write it with parens
• For example, we write (A, B) instead of {A, B}


• Thus, (A,B) = (B,A), etc


• If (A,B) ∈ E then (B,A) ∈ E


• Formally: ∀ u,v ∈ E, (u,v)=(v,u) and u ≠ v


• A node normally does not have an edge to itself

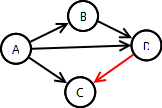
Directed Graphs

• Digraph: A graph whose edges are directed (ie have a direction)


• Edge drawn as arrow


• Edge can only be traversed in direction of arrow


• Example: E = {(A,B), (A,C), (A,D), (B,C), (D,C)}


• Examples: courses and prerequisites, program call graph


• In a digraph, an edge is an ordered pair
• Thus: (u,v) and (v,u) are not the same edge


• In the example, (D,C) ∈ E, (C,D) ∉ E


• What would edge (B,A) look like? Remember (A,B) ≠ (B,A)


• A node can have an edge to itself (eg (A,A) is valid)

Subgraph

• If graph G=(V, E)
• Then Graph G'=(V',E') is a subgraph of G if V' ⊆ V and E' ⊆ E and


• Example ...

Degree of a Node

• The degree of a node is the number of edges the node is used to define


• In the example above:
• Degree 2: B and C
• Degree 3: A and D


• A and D have odd degree, and B and C have even degree


• Can also define in-degree and out-degree
• In-degree: Number of edges pointing to a node
• Out-degree: Number of edges pointing from a node
• Whare are the in- and out-degree of the example?

Graphs: Terminology Involving Paths

• Path: sequence of vertices in which each pair of successive vertices is connected by an edge


• Cycle: a path that starts and ends on the same vertex


• Simple path: a path that does not cross itself
• That is, no vertex is repeated (except first and last)
• Simple paths cannot contain cycles


• Length of a path: Number of edges in the path
• Sometimes the sum of the weights of the edges


• Examples

• A sequence of vertices: (A, B, C, D) [Is this path, simple path, cycle?]
• (A, B, D, A, C) [path, simple path, cycle?]
• (A, B, D, A, C) [path, simple path, cycle?]
• Cycle: ?
• Simple Cycle: ?


• Lengths?

Cyclic and Acyclic Graphs

• A Cyclic graph contains cycles
• Example: roads (normally)


• An acyclic graph contains no cycles
• Example: Course prereqs!
• Examples - Are these cyclic or acyclic?

Connected and Unconnected Graphs and Connected Components

• An undirected graph is connected if every pair of vertices has a path between it
• Otherwise it is unconnected
• Give an example of a connected graph


• An unconnected graph can be broken in to connected components


• A directed graph is strongly connected if every pair of vertices has a path between them, in both directions

Trees and Minimum Spanning Trees

• Tree: undirected, connected graph with no cycles
• Example ...
• If G=(V, E) is a tree, how many edges in G?


• Spanning tree: a spanning tree of G is a connected subgraph of G that is a tree
• Example ...


• Minimum spanning tree (MST): a spanning tree with minimum weight
• Example ...


• Spanning trees and minimum spanning tree are not necessarily unique


• We will look at two famous MST algorithms: Prim's and Kruskal's

Data Structures for Representing Graphs

• Two common data structures for representing graphs:
• Adjacency lists
• Adjacency matrix

Adjacency List Representation

• Each node has a list of adjacent nodes


• Example (undirected graph):
• A: B, C, D
• B: A, D
• C: A, D
• D: A, B, C




• Example (directed graph):
• A: B, C, D
• B: D
• C: Nil
• D: C




• Weighted graph can store weights in list


• Space: Θ(V + E) (ie |V| + |E|)


• Time:
• To visit each node that is adjacent to node u: Θ(degree(u))
• To determine if node u is adjacent to node v: Θ(degree(u))

Adjacency Matrix Representation

• Adjacency Matrix: 2D array containing weights on edges
• Row for each vertex
• Column for each vertex
• Entries contain weight of edge from row vertex to column vertex
• Entries contain ∞ (ie Integer'last) if no edge from row vertex to column vertex
• Entries contain 0 on diagonal (if self edges not allowed)


• Example undirected graph (assume self-edges not allowed):

  	A	B	C	D
  A	0	1	1	1
  B	1	0	∞	1
  C	1	∞	0	1
  D	1	1	1	0

  
  


• Example directed graph (assume self-edges allowed):

  	A	B	C	D
  A	∞	1	1	1
  B	∞	∞	∞	1
  C	∞	∞	∞	∞
  D	∞	∞	1	∞

  
  


• Can store weights in cells


• Space: Θ(V²)


• Time:
• To visit each node that is adjacent to node u: Θ(V)
• To determine if node u is adjacent to node v: Θ(1)